Атомические разложения функций в пространстве Харди
Міністерство Освіти України
Одеський державний університет
ім. І.І.Мечнікова
Інститут математики, економіки та механіки
Атомічні розкладення функцій
у просторі Харді
Дипломна робота
студентки V курсу
факультету математики
Семенцовой В.А.
Науковий керівник
Вартанян Г.М.
Одеса - 2000
Содержание
Введение.................................................................................... 3
Глава I. Основные сведения об интеграле Пуассона и
пространствах ![]() ,
, ![]() и
и ![]() ................................. 8
................................. 8
§I.1. Интеграл Пуассона..................................................... 8
§I.2. Пространства ![]() ....................................................... 12
....................................................... 12
§I.3. Пространства ![]() и
и ![]() ......................................... 17
......................................... 17
§I.4. Произведение Бляшке, нетангенциальная
максимальная функция............................................... 22
Глава II. Атомические разложения функции в пространстве
![]() , пространство ВМО........................................ 26
, пространство ВМО........................................ 26
§II.1. Пространство ![]() , критерий принадлежности
, критерий принадлежности
функции из ![]() пространству
пространству ![]() ....................... 26
....................... 26
§II.2. Линейные ограниченные функционалы на ![]() ,
,
двойственность ![]() и ВМО.................................. 32
и ВМО.................................. 32
Литература.................................................................................. 37
Введение.
Целью настоящей работы является изучение основных понятий и результатов, полученных в области пространств Харди, которая не изучалась в рамках университетского курса. В работе прослежена взаимосвязь между следующими понятиями : интеграл Пуассона, пространства ![]() ,
, ![]() ,
, ![]() и
и ![]() , раскрыта суть и структура этих объектов. Описание указанных понятий вводится именно в такой последовательности , так как определение каждого последующего объекта дается на основе понятий, расположенных левее в выше перечисленном ряду объектов.
, раскрыта суть и структура этих объектов. Описание указанных понятий вводится именно в такой последовательности , так как определение каждого последующего объекта дается на основе понятий, расположенных левее в выше перечисленном ряду объектов.
Работа состоит из двух глав, каждая из которых делится на параграфы. В первой главе изучены свойства пространств ![]() ,
, ![]() ,
, ![]() , а во второй мы доказываем коитерий принадлежности функции из
, а во второй мы доказываем коитерий принадлежности функции из ![]() пространству
пространству ![]() и двойственность пространств
и двойственность пространств ![]() и
и ![]() .
.
В работе мы рассматриваем случай ![]() периодических функций. Используемые обозначения имеют следующий смысл:
периодических функций. Используемые обозначения имеют следующий смысл:
![]() - пространство
- пространство ![]() периодических, непрерывных на
периодических, непрерывных на ![]() функций;
функций;
![]() - пространство
- пространство ![]() периодических, бесконечно дифференцируемых на
периодических, бесконечно дифференцируемых на ![]() функций;
функций;
![]() - пространство
- пространство ![]() периодических, суммируемых в степени р на
периодических, суммируемых в степени р на ![]() функций, т.е.для которых
функций, т.е.для которых 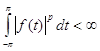 ,
, ![]() ;
;
![]() - пространство
- пространство ![]() периодических ограниченных на
периодических ограниченных на ![]() функций;
функций;
![]() - носитель функции
- носитель функции ![]() .
.
В §I.1.вводится понятие интеграла Пуассона: интегралом Пуассона суммируемой на (-p,p) 2p-периодической комплекснозначной функции ![]() называется функция
называется функция
¦r ( x ) = 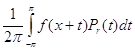 ,
,
где ![]() , t Î ( -p, p ) - ядро Пуассона.
, t Î ( -p, p ) - ядро Пуассона.
Здесь мы доказываем следующие свойства ядра Пуассона, которые мы неоднократно будем использовать в ряде доказательств:
а) ![]() ;
;
б) 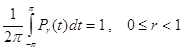 ;
;
в) для любого d>0
![]()
Основной целью данного параграфа являются две теоремы о поведении интеграла Пуассона ![]() при
при ![]() :
:
Теорема 1.
Для произвольной (комплекснозначной) функции ![]() ( -p, p ) , 1 £ p < ¥ , имеет место равенство
( -p, p ) , 1 £ p < ¥ , имеет место равенство![]()
![]() ;
;
если же ¦ (x) непрерывна на ( -p, p ) и ¦ (-p) = ¦ (p) , то
![]() .
.
Теорема 2 (Фату).
Пусть ![]() - комплекснозначная функция из
- комплекснозначная функция из ![]() . Тогда
. Тогда
![]() для п.в.
для п.в. ![]() .
.
В этом параграфе мы обращались к следующим понятиям:
Определение1. Функция ![]() называется аналитической в точке
называется аналитической в точке ![]() , если она дифференцируема в этой точке и в некоторой ее окрестности. Говорят, что функция
, если она дифференцируема в этой точке и в некоторой ее окрестности. Говорят, что функция ![]() аналитична на некотором множестве,если она аналитична в каждой точке этого множества.
аналитична на некотором множестве,если она аналитична в каждой точке этого множества.
Определение2. Действительная функция двух действительных переменных ![]() называется гармонической в области
называется гармонической в области ![]() , если
, если ![]() и удовлетворяет уравнению Лапласа:
и удовлетворяет уравнению Лапласа:
![]() .
.
Определение3. Две гармонические функции ![]() и
и ![]() , связанные условиями Коши-Римана :
, связанные условиями Коши-Римана : ![]() ,
, ![]() , называются гармонически сопряженными функциями.
, называются гармонически сопряженными функциями.
Определение4. Под нормой пространства ![]() понимается
понимается
![]() ,
, ![]() .
.
Определение5. Под нормой пространства ![]() понимается
понимается
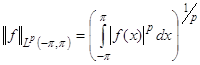 ,
, ![]() .
.
Определение6. Пусть ![]() ( или
( или ![]() ,
,![]() ). Модуль непрерывности ( соответственно интегральный модуль непрерывности) функции
). Модуль непрерывности ( соответственно интегральный модуль непрерывности) функции ![]() определяется равенством
определяется равенством
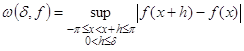 ,
, ![]() .
.
(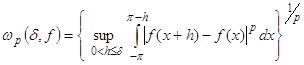 ,
, ![]() ).
).
Определение7. Последовательность ![]() функций, определенных на множестве Х с заданной на нем мерой, называется сходящейся почти всюду к функции
функций, определенных на множестве Х с заданной на нем мерой, называется сходящейся почти всюду к функции ![]() , если
, если ![]() для почти всех
для почти всех ![]() , т.е. множество тех точек
, т.е. множество тех точек ![]() , в которых данное соотношение не выполняется, имеет меру нуль.
, в которых данное соотношение не выполняется, имеет меру нуль.
В §I.2 мы рассматриваем пространства ![]() - это совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
- это совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
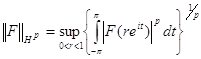 .
.
Основным результатом этого параграфа является теорема о том, что любую функцию ![]() (
(![]() ) можно предсавить в виде
) можно предсавить в виде
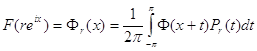 ,
, ![]() ,
, ![]() ,
,
где ![]() для п.в.
для п.в. ![]() , при этом
, при этом
![]()
![]() ;
;
![]()
![]() .
.
Использованные в данном параграфе понятия мы принимаем в следующих определениях:
Определение8. Говорят, что действительная функция ![]() , заданная на отрезке (a,b), имеет ограниченную вариацию, если существует такая постоянная
, заданная на отрезке (a,b), имеет ограниченную вариацию, если существует такая постоянная ![]() , что каково бы ни было разбиение отрезка (a,b) точками
, что каково бы ни было разбиение отрезка (a,b) точками ![]() выполнено неравенство
выполнено неравенство ![]() .
.
Определение9. Действительная функция ![]() , заданная на отрезке (a,b), называется абсолютно непрерывной на (a,b), если для любого
, заданная на отрезке (a,b), называется абсолютно непрерывной на (a,b), если для любого ![]() найдется число
найдется число ![]() такое, что какова бы ни была система попарно непересекающихся интервалов
такое, что какова бы ни была система попарно непересекающихся интервалов ![]() ,
, ![]() с суммой длин, меньшей
с суммой длин, меньшей ![]() :
: ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
В третьем параграфе первой главы мы переходим к рассмотрению пространств ![]() и
и ![]() . Пространство
. Пространство ![]() (
(![]() ) представляет собой совокупность тех функций
) представляет собой совокупность тех функций ![]() ,
, ![]() , которые являются граничными значениями функций (действительных частей функций) из
, которые являются граничными значениями функций (действительных частей функций) из![]() , т.е. представимы в виде
, т.е. представимы в виде ![]() (
(![]() ). Здесь мы получаем следующие результаты: при
). Здесь мы получаем следующие результаты: при ![]() пространство
пространство ![]() совпадает с
совпадает с ![]() , а при р=1
, а при р=1 ![]() уже, чем
уже, чем ![]() , и состоит из функций
, и состоит из функций ![]() , для которых и
, для которых и ![]() .
.
В §I.4 мы вводим понятие произведения Бляшке функции ![]() , аналитической в круге
, аналитической в круге ![]() с нулями
с нулями ![]() ,
, ![]() (
(![]() ) с учетом их кратности:
) с учетом их кратности:
![]() ,
,
где ![]() - кратность нуля функции
- кратность нуля функции ![]() при
при ![]() .
.
Здесь доказывается, что каждая функция ![]() представима в виде
представима в виде
![]() , где
, где ![]() не имеет нулей в круге
не имеет нулей в круге ![]() и
и ![]() ,
, ![]() ,а
,а ![]() - произведение Бляшке функции
- произведение Бляшке функции ![]() .
.
Затем мы рассматриваем понятие нетангенциальной максимальной функции . Пусть ![]() ,
, ![]() , - произвольное число. Обозначим через
, - произвольное число. Обозначим через ![]() ,
, ![]() , область, ограниченную двумя касательными, проведенными из точки
, область, ограниченную двумя касательными, проведенными из точки ![]() к окружности
к окружности ![]() , и наибольшей из дуг окружности, заключенных между точками касания ( при
, и наибольшей из дуг окружности, заключенных между точками касания ( при ![]()
![]() вырождается в радиус единичного круга). Для
вырождается в радиус единичного круга). Для ![]() положим
положим
![]() ,
, ![]() ,
,
где ![]() - интеграл Пуассона функции
- интеграл Пуассона функции ![]() . Функция
. Функция ![]() называется нетангенциальной максимальной функцией для
называется нетангенциальной максимальной функцией для ![]() .
.
Тут же мы доказываем теорему об оценке ![]() : если
: если ![]() (
(![]() ),
), ![]() , то
, то ![]() и
и ![]() .
.
Первые результаты о максимальных функциях были получены в 1930 году Харди и Литтлвудом.
Во второй главе два параграфа.
В §II.1 рассматривается пространство ![]() . Как ранее отмечалось, оно уже, чем
. Как ранее отмечалось, оно уже, чем ![]() . Поэтому в данном параграфе большой интерес представляет теорема - критерий принадлежности функции пространству
. Поэтому в данном параграфе большой интерес представляет теорема - критерий принадлежности функции пространству ![]() . Здесь вводится понятие атома: действительная функция
. Здесь вводится понятие атома: действительная функция ![]() называется атомом, если существует обобщенный интервал
называется атомом, если существует обобщенный интервал ![]() такой, что
такой, что
а) ![]() ; б)
; б)  ; в)
; в) ![]() .
.
Атомом назовем также функцию ![]() ,
, ![]() . Под обобщенным интервалом понимается либо интервал из
. Под обобщенным интервалом понимается либо интервал из ![]() , либо множество вида
, либо множество вида![]()
![]() (
(![]() ).
).
Данный параграф посвящен аналогу теоремы, доказанной в 1974 году Р.Койфманом о том, что функция ![]() тогда и только тогда, когда функция
тогда и только тогда, когда функция ![]() допускает представление в виде
допускает представление в виде
![]() ,
, ![]() , где
, где ![]() ,
, ![]() , - атомы. (*)
, - атомы. (*)
При этом ![]() , где inf берется по всем разложениям вида (*) функции
, где inf берется по всем разложениям вида (*) функции ![]() , а с и С
, а с и С ![]() - абсолютные константы.
- абсолютные константы.
Роль атомических разложений заключается в том, что они в ряде случаев позволяют свести вывод глубоких фактов к относительно простым действиям с атомами.
В частночти, из атомического разложения функций, принадлежащих пространству ![]() , легко вытекает полученный в 1971 году Ч.Фефферманом результат о двойственности пространств
, легко вытекает полученный в 1971 году Ч.Фефферманом результат о двойственности пространств ![]() и
и ![]() . Доказательству этого факта и посвящен второй параграф данной главы. Сперва мы вводим определение
. Доказательству этого факта и посвящен второй параграф данной главы. Сперва мы вводим определение ![]() : пространство ВМО есть совокупность всех функций
: пространство ВМО есть совокупность всех функций ![]() , удовлетворяющих условию
, удовлетворяющих условию
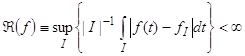 , (91)
, (91)
где ![]() , а sup берется по всем обобщенным интервалам
, а sup берется по всем обобщенным интервалам ![]() . А затем доказываем теорему о том, что
. А затем доказываем теорему о том, что ![]() .
.
Глава I.
Основные сведения об интеграле Пуассона и
пространствах ![]() ,
, ![]() и
и ![]()
§I.1.Интеграл Пуассона.
Пусть ¦(x) , g(x) , xÎR1 –суммируемые на (-p, p) , 2p- периодические, комплекснозначные функции. Через f*g(x) будем обозначать свертку
![]() f*g(x) =
f*g(x) =![]()
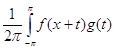 dt
dt![]()
![]()
![]()
![]()
Из теоремы Фубини следует, что свертка суммируемых функций также суммируема на (-p,p) и
cn ( f*g ) = cn ( f )× c-n ( g ) , n = 0, ±1 , ±2 , ... ( 1 )
где { cn ( f )} - коэффициенты Фурье функции f ( x ) :
cn (f)= 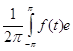 -i n tdt , n = 0, ±1, ±2,¼
-i n tdt , n = 0, ±1, ±2,¼
Пусть ¦ Î L1 (-p, p ) . Рассмотрим при 0 £ r < 1 функцию
¦r ( x ) = ![]() n ( f ) r|n | ei n x , x Î ( -p, p ) . ( 2 )
n ( f ) r|n | ei n x , x Î ( -p, p ) . ( 2 )
Так как ![]() для любых x Î ( -p, p ), n = 0, ±1, ±2,¼, а ряд
для любых x Î ( -p, p ), n = 0, ±1, ±2,¼, а ряд ![]() сходится (так как согласно теореме Мерсера (4) коэффициенты Фурье любой суммируемой функции по ортогональной системе ограниченных в совокупности функций
сходится (так как согласно теореме Мерсера (4) коэффициенты Фурье любой суммируемой функции по ортогональной системе ограниченных в совокупности функций ![]() стремятся к нулю при
стремятся к нулю при ![]() ), то по признаку Вейерштрасса ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦r (х) равны cn ( fr ) = cn (f)× r| n | , n = 0 , ±1, ±2, ¼ , а это значит, что ¦r ( x ) можно представить в виде свертки :
), то по признаку Вейерштрасса ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦r (х) равны cn ( fr ) = cn (f)× r| n | , n = 0 , ±1, ±2, ¼ , а это значит, что ¦r ( x ) можно представить в виде свертки :![]()
¦r ( x ) = 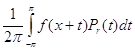 , ( 3 )
, ( 3 )
где
![]() , t Î ( -p, p ) . ( 4 )
, t Î ( -p, p ) . ( 4 )
Функция двух переменных Рr (t) , 0 £ r <1 , t Î ( -p, p ) , называется ядром Пуассона , а интеграл (3) - интегралом Пуассона .
![]()
![]()
![]()
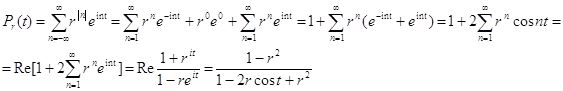
![]()
Следовательно,
Pr ( t ) = ![]() , 0 £ r < 1 , t Î ( -p, p) . ( 5 )
, 0 £ r < 1 , t Î ( -p, p) . ( 5 )
Если ¦Î L1 ( -p, p ) - действительная функция , то , учитывая , что
c-n ( f ) = ![]() , n = 0, ±1, ±2,¼, из соотношения (2) мы получим :
, n = 0, ±1, ±2,¼, из соотношения (2) мы получим :
fr ( x ) = ![]()
=![]() , ( 6 )
, ( 6 )
где
F ( z ) = c0 ( f ) + 2 ![]() ( z = reix ) ( 7 )
( z = reix ) ( 7 )
- аналитическая в единичном круге функция как сумма равномерно сходящегося по х ряда (5). Равенство (6) показывает, что для любой действительной функции ¦Î L1( -p, p ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция
u ( z ) = ¦r (eix ) , z = reix , 0 £ r <1 , x Î ( -p, p ) .
При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой
v (z) = Im F (z) = ![]() . ( 8 )
. ( 8 )
Утверждение1.
Пусть u (z) - гармоническая ( или аналитическая ) в круге | z | < 1+e ( e>0 ) функция и ¦ (x) = u (eix) , xÎ( -p, p ) . Тогда
u (z) = 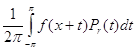 ( z = reix , | z | < 1 ) ( 10 )
( z = reix , | z | < 1 ) ( 10 )
Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:
![]() =
=![]() , | z | < 1+ e .
, | z | < 1+ e .
Но тогда коэффициенты Фурье функции ![]() связаны с коэффициентами Фурье функции
связаны с коэффициентами Фурье функции ![]() следующим образом :
следующим образом :
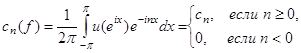
и равенство (10) сразу следует из (2) и (3).
Прежде чем перейти к изучению поведения функции ¦r (x) при r®1 , отметим некоторые свойства ядра Пуассона:
а) ![]() ;
;
б) 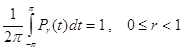 ; (11)
; (11)
в) для любого d>0
![]()
Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦ (х) º 1.![]()
Теорема 1.
Для произвольной (комплекснозначной) функции ![]() ( -p, p ) , 1 £ p < ¥ , имеет место равенство
( -p, p ) , 1 £ p < ¥ , имеет место равенство![]()
![]() ;
;
если же ¦ (x) непрерывна на ( -p, p ) и ¦ (-p) = ¦ (p) , то
![]() .
.
Доказательство.
В силу (3) и свойства б) ядра Пуассона
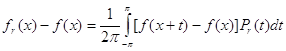 . ( 12 )
. ( 12 )
Для любой функции ![]() , пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим
, пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим![]()
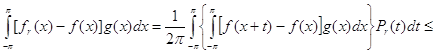
![]()
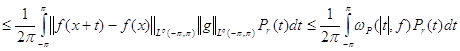 .
.
Следовательно,
![]()
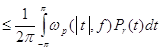 .
.
Для данного e > 0 найдем d = d (e) такое, что ![]() . Тогда для r , достаточно близких к единице, из свойств а)-в) мы получим оценку
. Тогда для r , достаточно близких к единице, из свойств а)-в) мы получим оценку
![]()
![]()
![]() .
.
Аналогично, второе утверждение теоремы 1 вытекает из неравенства
![]()
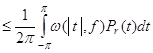 .
.
Теорема 1 доказана.
Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.
ОпределениеI.1.
Пусть функция ![]() , суммируема на любом интервале (a,b), a
, суммируема на любом интервале (a,b), a![]() называется функция
называется функция
![]() ,
,
где супремум берется по всем интервалам I , содержащим точку х.
Определение I.2.
Оператор ![]() называется оператором слабого типа (р,р) , если для любого y > 0
называется оператором слабого типа (р,р) , если для любого y > 0
![]() ,
, ![]() .
.
Теорема 2 (Фату).
Пусть ![]() - комплекснозначная функция из
- комплекснозначная функция из ![]() . Тогда
. Тогда
![]() для п.в.
для п.в. ![]() .
.
Доказательство.
Покажем, что для ![]() и
и ![]()
![]() , ( 13 )
, ( 13 )
где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x)*). Для этой цели используем легко выводимую из (5) оценку
![]()
(К - абсолютная константа).
Пусть ![]() - такое число, что
- такое число, что
![]() .
.
Тогда для ![]()
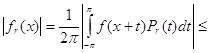
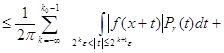
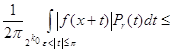
![]()
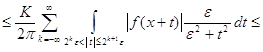
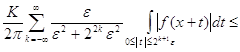
![]() .
.
Неравенство (13) доказано. Возьмем слабый тип (1,1) оператора ![]() . Используя его, найдем такую последовательность функций
. Используя его, найдем такую последовательность функций ![]() ,что
,что
![]() ,
,
![]() ( 14 )
( 14 )
![]() для п.в.
для п.в. ![]() .
.
Согласно (13) при xÎ (-p,p)
![]()
![]()
Учитывая , что по теореме 1 ![]() для каждого xÎ (-p, p) и (14)
для каждого xÎ (-p, p) и (14)
из последней оценки получим
![]() при r®1.
при r®1.
Теорема 2 доказана.
Замечание1.
Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ (-p, p) ![]() , когда точка reit стремится к eix по некасательному к окружности
, когда точка reit стремится к eix по некасательному к окружности ![]() пути.
пути.
§I.2.Пространства Hp.![]()
Определение I.3.
Пространство ![]() - совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
- совокупность аналитических в единичном круге функций F (z) , для которых конечна норма
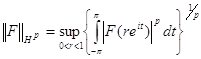 . (15)
. (15)
Пусть комплекснозначная функция ![]() удовлетворяет условиям
удовлетворяет условиям
![]()
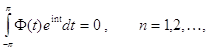 (16)
(16)
тогда функция F (z) , определенная равенством
 (17)
(17)
принадлежит пространству ![]() , причем
, причем
![]() . (18)
. (18)
![]()
![]() Действительно, аналитичность функции F (z) следует из (16) и равенства (2). Кроме того, в силу неравенства
Действительно, аналитичность функции F (z) следует из (16) и равенства (2). Кроме того, в силу неравенства ![]() мы имеем
мы имеем
 (*)
(*)
С другой стороны , по теореме 1 ( а при р=¥ в силу теоремы 2)
![]() . Отсюда
. Отсюда ![]() (**)
(**)
Учитывая (*) и (**) , получим (18).
Ниже мы докажем, что любую функцию ![]()
![]() можно представить в виде (17). Для этого нам потребуется
можно представить в виде (17). Для этого нам потребуется
Теорема 3.
Пусть комплекснозначная функция j (t) имеет ограниченную вариацию на ( -p,p) и
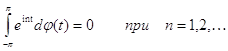 (19)
(19)
Тогда j (t) абсолютно непрерывна на (-p,p).
Замечание2.
В (19) и ниже рассматривается интеграл Лебега-Стилтьеса, построенный по комплекснозначной функции ограниченной вариации j (t) . Мы говорим, что
j (t)= u (t)+ i v (t) имеет ограниченную вариацию (абсолютно непрерывна), если обе действительные функции u (t) и v (t) имеют ограниченную вариацию (соответственно абсолютно непрерывны). При этом интеграл
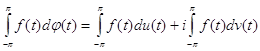
определен для каждой непрерывной на (-p,p) функции f (t) , а также если
![]() - характеристическая функция замкнутого множества
- характеристическая функция замкнутого множества ![]() .
.
Доказательство теоремы 3.
Нам достаточно проверить, что для любого замкнутого множества ![]() ,
,
![]() ,
,
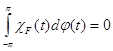 (20)
(20)
Для этой цели убедимся, что справедлива
Лемма 1.
Пусть F - замкнутое, а V - открытое множества , причем ![]() и
и
![]() . Тогда для всякого
. Тогда для всякого ![]() , существует функция
, существует функция ![]() вида
вида
![]() , (21)
, (21)
обладающая свойствами:
а) ![]() ;
;
б) ![]() ; (22)
; (22)
в) ![]() .
.
Выведем из леммы 1 оценку (20), а затем докажем саму лемму 1.
Пусть ![]() , где
, где ![]() - конечная или бесконечная последовательность дополнительных интервалов множества F, и для
- конечная или бесконечная последовательность дополнительных интервалов множества F, и для ![]()
![]() .
.
Очевидно, что ![]() - открытое множество и
- открытое множество и ![]() .
.
Рассмотрим для данных ![]() функцию
функцию ![]() , построенную в лемме 1 для числа e и множества
, построенную в лемме 1 для числа e и множества ![]() . Тогда нетрудно проверить(3), что если
. Тогда нетрудно проверить(3), что если ![]() , а
, а ![]() , то разность
, то разность
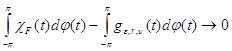 . (23)
. (23)
Но в силу (19) и равномерной сходимости ряда (21) (так как ряд Фурье бесконечно дифференцируемой функции сходится равномерно)
 ,
,
и мы получаем равенство (20).
Перейдем к доказательству леммы 1. Нам понадобится
ОпределениеI.4.
Средние Фейера - это средние вида
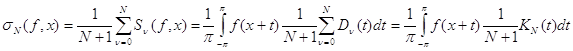
![]() , где
, где ![]() ,
, ![]() ,
, ![]() - ядро Дирихле,
- ядро Дирихле,
![]() ,
, ![]() - ядро Фейера.
- ядро Фейера.
Отметим, что при ![]() ядро Фейера обладает следующими свойствами: а)
ядро Фейера обладает следующими свойствами: а) ![]() ,
, ![]() ; б)
; б) 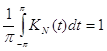 ,
,
Мз которых вытекает, что для ![]() и
и ![]()
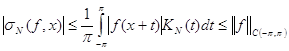 ,
, ![]()
Также известно (3), что средние Фейера ![]() равномерно сходятся к
равномерно сходятся к ![]() .
.
Пусть f(t) - непрерывная на (-p, p) функция, для которой
![]()
![]() и
и ![]()
Так как средние Фейера ![]() равномерно сходятся к
равномерно сходятся к ![]() и
и
![]() , то существует тригонометрический полином
, то существует тригонометрический полином
![]() (24)
(24)
такой, что
![]() (25)
(25)
Пусть ![]() . Рассмотрим для каждого d>0 такую функцию
. Рассмотрим для каждого d>0 такую функцию ![]() , что
, что
![]() ,
, ![]()
![]()
(функцию ![]() можно построить следующим образом: взять замкнутое множество
можно построить следующим образом: взять замкнутое множество ![]() с мерой
с мерой ![]() , достаточно близкой к 2p, и положить
, достаточно близкой к 2p, и положить
![]() ).
).
Так как ![]() (здесь число m то же, что в (24)), то для достаточно малых d>0 функция
(здесь число m то же, что в (24)), то для достаточно малых d>0 функция ![]() удовлетворяет соотношениям
удовлетворяет соотношениям
![]() (26)
(26)
При этом ![]() , если
, если ![]() . Тогда средние Фейера
. Тогда средние Фейера ![]() функции h(t) имеют вид
функции h(t) имеют вид
![]()
и при достаточно большом N
![]() (27)
(27)
Положим
![]() ,
, ![]() (28)
(28)
Так как h(t) - действительная функция, то ![]() , n=0,±1,±2,¼. Поэтому
, n=0,±1,±2,¼. Поэтому
![]() и
и ![]() . (29)
. (29)
Определим искомую функцию g(t) :
![]()
Ясно, что ![]() , а из (24) и (28) следует, что
, а из (24) и (28) следует, что ![]() при n<0, т.е.
при n<0, т.е.
![]() (30)
(30)
В силу соотношений (25), (27) и (29) для ![]()
![]() ,
,
а для ![]()
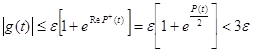 .
.
Наконец, для любого ![]()
![]() .
.
Таким образом, функция g(t) обладает всеми нужными свойствами (22). Лемма1 , а вместе с ней и теорема 3 доказаны.
Теорема 4.
Пусть функция ![]() . Тогда для п.в.
. Тогда для п.в. ![]() существует предел
существует предел
![]() (31)
(31)
При этом
1) 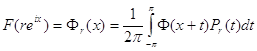 ,
, ![]() ,
, ![]() ;
;
2) ![]()
![]() ;
;
3) ![]()
![]() .
.
Доказательство:
Нам достаточно доказать, что для каждой функции ![]() найдется функция
найдется функция ![]() такая, что имеет место 1). Действительно, если
такая, что имеет место 1). Действительно, если ![]() , то тем более
, то тем более ![]() и из 1) и теоремы 2 вытекает справедливость равенства (31) для п.в.
и из 1) и теоремы 2 вытекает справедливость равенства (31) для п.в. ![]() . При этом
. При этом ![]() и по теореме 1
и по теореме 1 ![]()
![]() . Наконец, из 1) следует, что
. Наконец, из 1) следует, что
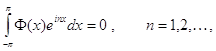
а тогда
![]() .
.
Пусть ![]() . Для построения искомой функции
. Для построения искомой функции ![]() положим
положим
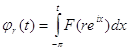 ,
, ![]() ,
, ![]() .
.
Функции ![]() ,
, ![]() , имеют равномерно ограниченную по r вариацию на
, имеют равномерно ограниченную по r вариацию на ![]() :
:
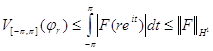 .
.
Следовательно, по теореме Хелли (2) найдутся функция ограниченной вариации ![]() и последовательность
и последовательность ![]() , такие, что
, такие, что ![]() в каждой точке
в каждой точке ![]() и
и
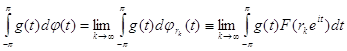 (32)
(32)
для любой функции ![]() . При этом для n=1,2,...
. При этом для n=1,2,...
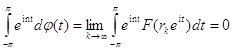
(мы учли аналитичность функции F(z) в единичном круге) и , следовательно, по теореме 3 ![]() абсолютно непрерывна : существует функция
абсолютно непрерывна : существует функция ![]() , для которой
, для которой
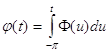 ,
, ![]()
Тогда
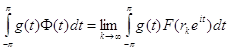 ,
, ![]() (33)
(33)
Зафиксируем число ![]() . Функция
. Функция ![]() , аналитична в круге
, аналитична в круге 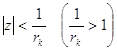 , поэтому согласно утверждению 1
, поэтому согласно утверждению 1
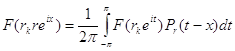 ,
, ![]() .
.
В пределе при ![]() из последнего равенства вытекает, что
из последнего равенства вытекает, что
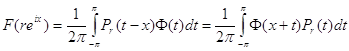 ,
, ![]() ,
, ![]() .
.
Равенство 1) , а вместе с ним и теорема 4 доказаны.
§I.3.Пространства ![]() и
и ![]() .
.
Обозначим через ![]()
![]() класс тех функций
класс тех функций ![]() ,
, ![]() , которые являются граничными значениями функций из
, которые являются граничными значениями функций из ![]() , т.е. представимы в виде
, т.е. представимы в виде
![]() для п.в.
для п.в. ![]() ,
, ![]() .
.
В силу пунктов 3) и 2) теоремы 4 ![]() и каждая функция
и каждая функция ![]() удовлетворяет условию (16). С другой стороны, выше мы доказали, что для произвольной
удовлетворяет условию (16). С другой стороны, выше мы доказали, что для произвольной ![]() с условием (16) интеграл Пуассона (17) определяет функцию из
с условием (16) интеграл Пуассона (17) определяет функцию из ![]() . Следовательно,
. Следовательно,
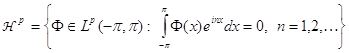 . (34)
. (34)
Из (34) вытекает, что ![]() (замкнутое) - подпространство пространства
(замкнутое) - подпространство пространства ![]() , а
, а ![]() - банахово пространство с нормой (15).
- банахово пространство с нормой (15).
Пусть ![]() . Положим
. Положим
![]() ,
,
 , (35)
, (35)
![]()
ОпределениеI.5.
Если функция ![]() , то сопряженной к ней функцией называется функция
, то сопряженной к ней функцией называется функция 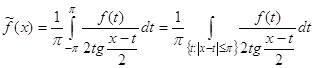 ,
, ![]() ,
,
где интеграл понимается в смысле главного значения, т.е. как предел при ![]() интегралов
интегралов 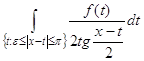 .
.
В дальнейшем нам понадобится
Утверждение2.
Для любой функции ![]() сопряженная функция
сопряженная функция ![]() существует и конечна п.в. на
существует и конечна п.в. на ![]() ; при этом
; при этом
а) ![]() , y>0;
, y>0;
б) если ![]() ,
, ![]() , то
, то ![]() и
и ![]() .
.
Теорема 5.
Следующие условия эквивалентны ![]() :
:
а) ![]() ;
;
б) ![]() ,
, 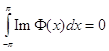 ,
, 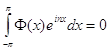 ,
, ![]() ;
;
в) 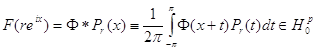 ;
;
г) ![]() , где
, где ![]() - такая действительная функция, что ее сопряженная
- такая действительная функция, что ее сопряженная ![]() также принадлежит пространству
также принадлежит пространству ![]() :
:
 . (36)
. (36)
Доказательство:
Эквивалентность условий а) и б) непосредственно вытекает из (34), а эквивалентность условий а) и в) - из теорем 4 и 2.
Докажем, что из г) следует б). Для этого достаточно проверить, что в случае, когда функция и ее сопряженная суммируемы :![]() , имеют место равенства
, имеют место равенства
![]() ,
, ![]() (37)
(37)
Непосредственный подсчет по формуле (36) показывает, что
![]() ,
, ![]() ,
, ![]() ,
, ![]()
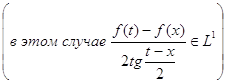 . Следовательно, равенства (37) выполняются, если
. Следовательно, равенства (37) выполняются, если ![]() - произвольный тригонометрический полином.
- произвольный тригонометрический полином.
Пусть ![]() фиксировано. Для произвольной функции
фиксировано. Для произвольной функции ![]() и
и ![]() положим
положим
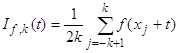 ,
, 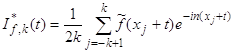 ,
,
где ![]() ,
, ![]() ,
, ![]() .
.
Покажем, что равенство (37) для фиксированного нами номера n вытекает из следующих свойств функций ![]() (наличие эт
(наличие эт