Проблема движения

Классификация форм движения.

В широком смысле понятие движение используется для обозначения любых изменений, происходящих с объектом или системой объектов с течением времени. Различным уровням организации материи соответствуют свои характерные формы движения (социальные, биологические, химические, физические и т.д.). Высшие формы движения включают в себя более простые и могут быть сведены к их совокупностям (напр. передача возбуждения между нервными клетками организма представляет собой импульсы токов и напряжений, распространяющихся по нейронам, а последние обусловлены движением положительно заряженных ионов Na и K). Простейшей формой является механическое движение, представляющее собой перемещение объектов в пространстве.

Описание изменяющихся во времени величин. Если какая-либо величина F, которой может быть приписано численное значение, изменяется во времени, это символически записывают в следующем виде:

(1)  .

Существует несколько способов задания зависимости F(t), соответствующих различным уровням экспериментального изучения явлений.

Табличный способ представляет собой набор численных значений измеряемой величины  в моменты времени  и наиболее достоверно отражает результаты измерений. В связи с тем, что измеряемые величины не могут быть определены абсолютно точно, корректная запись результатов измерений должна содержать информацию о погрешности в виде доверительного интервала, т.е. численного промежутка, в котором находится истинное значение измеряемой величины с заранее заданной вероятностью (обычно 90%). Ниже приводится пример табличного задания роста ребенка во времени по результатам измерений, проводившихся по одному разу в год в месяц его рождения:

Возраст (годы) Рост (метры)

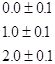
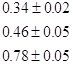
Основным недостатком этого способа является его малая наглядность.

Графический способ состоит в нанесении точек на график, по осям которого отложены значения величин F и t. “Точки” положено изображать в виде фигур (прямоугольников, эллипсов, крестиков и т.д.), размеры которых отражают погрешность измерений (рис. 3_1). Обычно нанесенные точки соединяют плавной кривой, отражающей представления исследователя (часто весьма субъективные) о истинном характере зависимости F(t). Интервал между точками на графиках желательно выбирать так, чтобы между ними изображаемая зависимость имела монотонный характер, т.е. не имела минимумов и максимумов.

Аналитический способ представляет собой описание зависимости F(t) в виде функции, конкретный вид которой подбирается на основе разумного компромисса между требованиями наилучшего соответствия с результатами измерений и простоты формул. Часто качественный вид зависимости априорно известен из теории. При этом выбор рассматриваемых функций существенно сужается, результаты измерений частично учитываются подбором значений подгоночных параметров. Последний способ задания наиболее информативен, но наименее достоверен.

Производная и интеграл.

Для характеристики изменения величины F(t) вводится понятие скорости ее изменения (отношение приращения величины к соответствующему интервалу времени при условии, что последний весьма мал):

(2)  .

Для математической операции (2), носящей название дифференцирования или взятия производной, используется несколько общепринятых обозначений:

(3)  .

Величина производной числено равна тангенсу угла наклона касательной к графику F(t) (рис. 3_2). В случае возрастания функции F ее производная положительна, при убывании - отрицательна. В точках экстремумов (минимумов и максимумов) производная обращается в нуль. По известной зависимости F(t) производная всегда вычисляется и при том - однозначно (исключение составляют лишь случаи, когда F(t) имеет разрывы, но в реальной природе подобных зависимостей практически никогда не встречается).

Обратная задача- определение зависимости F(t) по известной скорости ее изменения  имеет однозначное решение лишь в случае дополнительного задания начального условия (значения величины F в какой-либо момент времени):

(4)  .

Приращение величины F вычисляется в результате взятия определенного интеграла:

(5)  ,

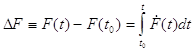числено равного площади под графиком зависимости  (рис. 3_2). По приращению величины и ее значению, согласно (5), можно найти F(t):

(6)  .

Описание эволюции сложных систем. Системы, имеющие несколько степеней свободы, описываются набором величин  называемых координатами системы (число координат N равно числу степеней свободы). Геометрическим образом состояния системы является точка в N-мерном пространстве конфигураций, координаты которой определяются набором . Если система изменяется с течением времени, составляющие набора  изменяются и изображающая точка перемещается в конфигурационном пространстве =(t).

Векторные и скалярные величины.

C математической точки зрения вектором можно называть упорядоченный набор чисел лишь в том случае, если он обладает рядом определенных свойств. В частности, для любых двух таких наборов должны быть определены операции сложения и умножения на число так, чтобы выполнялись следующие свойства:

коммутативности:

(7)  ,  ,

ассоциативности:

(8)  ,  ,

и дистрибутивности:

(9)  ,  ,

Поскольку свойства (7-9) справедливы для операций сложения и умножения вещественных чисел, практически все утверждения из алгебры скалярных величин остаются справедливыми и для векторов. Вектор является обобщением понятия числа на случай многомерных пространств. Скаляры можно рассматривать как векторы в одномерном пространстве.

Использование векторов позволяет строить описание весьма разнообразных объектов (материальных точек, сил, полей, состояний, численности населения городов, физиологических ощущений и т.д.), используя единообразные математические обозначения

Пользуясь аналогией с соотношениями (1-6), легко определить понятие вектора скорости изменения системы:

(10)

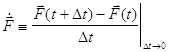
и обобщить все последующие соотношения на многомерный случай.

Движение материальной точки в пространстве трех измерений является частным примеров эволюции во времени весьма простой системы, исчерпывающее описание которой дается тремя декартовыми координатами, совокупность которых называется радиус-вектором:

(11)

(для обозначения “обычных” векторов в трехмерном пространстве будут использоваться жирные буквы без стрелок).

Сумма векторов определяется как вектор, составляющие которого являются суммами соответствующих составляющих слагаемых

(12)  ,

а произведение на число - как вектор, составляющие которого получаются домножением составляющих исходного на это число:

(13)  .

Легко убедиться, что все необходимые свойства (7-9) при таком определении операций выполняются. Производная радиус-вектора по времени получила название вектора мгновенной скорости:

(14)  ,

а производная скорости - ускорения:

(15)  .

По известной зависимости положения тела от времени R(t) его скорость и ускорение определяются однозначно. В случае заданной скорости V(t) для однозначного определения радиус-вектора R(t) необходимо знать положение тела в какой-то определенный момент времени (“начальное положение”). Если же задана зависимость ускорения от времени, то по ней может быть найдена скорость, а по последней - радиус-вектор. Очевидно, что решение будет однозначным, если заданы начальная скорость и положение тела.

Относительность механического движения. Однозначное задание радиус-вектора возможно лишь после задания системы координат. Различные системы координат могут по-разному располагаться в пространстве и иметь различные скорости движения. Получим связь между характеристиками движения материальной точки в неподвижной (0) и движущейся (0’) системах отсчета (рис. 3_3) . Пусть R(t) и R’(t) - радиус-векторы материальной точки в двух системах отсчета, а r(t) - вектор, задающий положений движущейся системы (0’) относительно неподвижной (0). Очевидно, что

(16)  .

Дифференцируя равенство (16) по времени, получаем закон сложение скоростей, позволяющий находить скорость относительно движущейся системы отсчета V’, если заданы скорость движения тела в неподвижной V и относительная скорость движения систем отсчета v:

(17)  .

Аналогичное соотношение справедливо и для ускорений.

Закон (10) показывает, что тело, покоящееся в одной системе отсчета, может двигаться в другой. Т.о. бессмысленно говорить о механическом движении вообще, не указав системы отсчета. Говорят, что механическое движение относительно.

Закон преобразования координат (16), записанный для частного случая равномерного прямолинейного движения одной системы отсчета относительно другой (рис. 3_4) носит название преобразований Галилея:

(18)  .

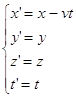Приведенные соотношения с точки зрения здравого смысла кажутся самоочевидными. На сомом деле при их выводе делаются весьма сильные допущения о том, что интервалы времени и длины отрезков одинаковы в обоих системах отсчета.

Эффект Доплера, являющийся следствием закон сложения скоростей, имеет много интересных проявлений в природе и технике. Пусть какой-либо источник создает с частотой  периодическое возмущение (“сигнал”) , распространяющееся в пространстве со скоростью C (примером может служить распространение звуковых волн в воздухе). Эффект Доплера состоит в том, что в случае движения источника или приемника частота принимаемого сигнала изменяется. Пусть, например, источник приближается к неподвижному приемнику со скоростью V. Скорость движения сигнала относительно источника, согласно (17), равна c’=c-v. За время между излучением двух последовательных сигналов  пройденный возмущением путь окажется равным (рис. 3_5). Приемник будет регистрировать приход сигналов через время , т.е. с частотой

(18)  .

При удалении источника (V<0) регистрируемая частота оказывается меньше исходной (звук, например, будет казаться более низким), при приближении (V>0) - частота возрастает (звук становится более высоким). В случае V=C частота становится бесконечно большой, что в акустике соответствует возникновению ударной волны при движении источника со скоростью звука (т.н. звуковой барьер). При сверхзвуковом движении формула (18) формально дает отрицательное значение частоты, что соответствует приему сигналов, приходящих в обратном порядке по сравнению с их испусканием.

В оптике наблюдается сходный эффект, приводящий к изменению частоты излучения (цвета) источника: удаляющиеся источники выглядят “более красными”, приближающиеся - “фиолетовыми” Количественные соотношения несколько отличаются от (18), поскольку при решении задач о движении с около световыми скоростями закон сложения скоростей (17) перестает выполняться. Астрономические наблюдения показывают, что спектры излучения далеких звезд смещены в красную сторону (т.е. частота приходящего от далеких звезд света оказывается заниженной), что служит основой для предположения о разбегании галактик или расширении Вселенной. Измерения сдвигов частот показали, что скорости разбегания звезд пропорциональны расстояниям до них (рис. 3_6):

(19) ,

где константа H носит названия постоянной Хаббла.

Утверждение о разбегании галактик ставит два естественных вопроса:

1) Не означает ли соотношение (19) что мы находимся в центре мира?

2) Куда разбегаются звезды?

Ответ на первый вопрос достаточно очевиден: наблюдатель на любой другой звезде увидит точно такую же картину разбегания. Например, скорость звезды 1 относительно звезды 2, согласно закону сложения скоростей равна

(20)  ,

что соответствует закону Хаббла. (рис. 3_5).

Удовлетворительный ответ на второй вопрос, попутно разрешающий парадокс звездного неба, по-видимому состоит в утверждении о глобальной неэвклидовости нашего пространства. Сказанное можно пояснить на модели двумерных существ, оказавшихся на поверхности сферы, радиус которой возрастает во времени (надувающийся шарик). Если на поверхность такой сферы нанести точки (“звезды”), расстояние между ними будет увеличиваться в полном соответствии с законом Хаббла (прямыми в этом “искривленном мире” следует называть дуги больших кругов на поверхности сферы). Вопрос же о том, куда разбегаются звезды для двумерных существ вообще бессмысленен, поскольку они не способны даже представить истинного вида поверхности, на которой находятся.