Метод расчета скейлинговых констант Фейгенбаума для одномерных дискретных отображений по точкам сверхустойчивых циклов
Антон Никифоров
Напомню для начала некоторые факты из теории универсальности Митчелла Фейгенбаума. Будем называть непрерывное отображение отрезка в себя унимодальным, если внутри отрезка имеется точка экстремума ![]() и по обе стороны от неё отображение является строго монотонным (с одной из сторон возрастающим, с другой убывающим). Условимся далее рассматривать только унимодальные отображения вида
и по обе стороны от неё отображение является строго монотонным (с одной из сторон возрастающим, с другой убывающим). Условимся далее рассматривать только унимодальные отображения вида
| (1) |
Если последовательность {![]() } при данном r состоит из n точек, такую последовательность будем называть n-циклом, что
} при данном r состоит из n точек, такую последовательность будем называть n-циклом, что ![]() =f(
=f(![]() ),
), ![]() =f(
=f(![]() ), …,
), …, ![]() =f(
=f( ![]() ) или
) или ![]() . Заметим, что производная порядка n функции
. Заметим, что производная порядка n функции ![]() (n раз вычисленной функции f(x)) в точке x по правилу дифференцирования сложной функции равна
(n раз вычисленной функции f(x)) в точке x по правилу дифференцирования сложной функции равна ![]() .
.
Точки цикла, удовлетворяющие соотношению
| (2) |
называются неподвижными.
Величина ![]() (так называемый мультипликатор) определяет устойчивость n-цикла и её принято называть устойчивостью (stability, (2), p.121). n-цикл называется устойчивым, если
(так называемый мультипликатор) определяет устойчивость n-цикла и её принято называть устойчивостью (stability, (2), p.121). n-цикл называется устойчивым, если ![]() <1.
<1.
n-цикл, содержащий ![]() в качестве одной из своих точек, называются сверхустойчивым. Для такого цикла
в качестве одной из своих точек, называются сверхустойчивым. Для такого цикла ![]() =0.
=0.
Как было продемонстрировано в 1978 году М.Фейгенбаумом (4), значения параметра ![]() , при которых число устойчивых периодических точек удваивается и становится равным
, при которых число устойчивых периодических точек удваивается и становится равным ![]() , удовлетворяют масштабному соотношению, или как говорят имеют скейлинг:
, удовлетворяют масштабному соотношению, или как говорят имеют скейлинг:
| (3) |
Данное соотношение встречается также и в следующей записи:
| (3.1) |
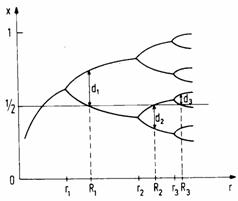
Рис.1 | Или в таком виде:
Расстояния
Константы Фейгенбаума имеют значения |
Сказку о том, как Фейгенбаум сидел в тени деревьев и вычислял их на своём калькуляторе HP-65 с золотистыми кнопочками вы, наверное, слышали. Это был первый программируемый калькулятор и стоил ни много ни мало аж 400 (четыреста!) долларов. Наивно полагать, что своё удивительное открытие Фейгенбаум сделал, пользуясь исключительно калькулятором: все-таки в то время он работал в Лос-Аламосе, а у военных всегда были и будут самые мощные компьютеры в мире, однако открытие действительно было чудесным - какие бы унимодальные отображения мы не рассматривали, скейлинг для них (т.е. "волшебные" числа ![]() и
и ![]() ) будет тем же самым.
) будет тем же самым.
Алгоритм
Интересно, что точки ![]() также можно использовать для расчета
также можно использовать для расчета ![]() , этим факт мы и будем использовать в дальнейшем. Обратим внимание, что в точках
, этим факт мы и будем использовать в дальнейшем. Обратим внимание, что в точках ![]() мультипликатор
мультипликатор ![]() всегда равен нулю, что автоматически означает устойчивость этих циклов:
всегда равен нулю, что автоматически означает устойчивость этих циклов:
![]()
| (a) | Например, для цикла периода два: | |
| ||
| ||
| (5.1) |
| (б) | Цикл периода четыре: | |
| ||
| ||
| (5.2) |
Для произвольных же ![]() -циклов справедливо выражение:
-циклов справедливо выражение:
| (6) |
Уравнение (5.3) легко решается относительно параметра ![]() , например, с помощью метода последовательных итераций Ньютона:
, например, с помощью метода последовательных итераций Ньютона:
| (6.1) |
Здесь i - номер итерации. Таким образом, весь процесс вычисления, скажем, константы ![]() сводится к нахождению таких значений параметра R, при которых бифуркационная диаграмма пересекает линию
сводится к нахождению таких значений параметра R, при которых бифуркационная диаграмма пересекает линию ![]() . Для этого необходимо решить уравнение (6), проитерировав его
. Для этого необходимо решить уравнение (6), проитерировав его ![]() раз.
раз.
НА ВХОД ПОДАЕМ:
Начинаем итерировать функцию f cо следующего значения: ![]()
Итерируем производную функции начиная с ![]()
Начальные приближения двух значений параметра R: ![]() ,
, ![]()
Разумное начальное приближение для постоянной : ![]()
НА ВЫХОДЕ ПОЛУЧАЕМ:
![]()
А весь процесс может быть описан следующими выражениями:
![]() , n=2,3,4,…
, n=2,3,4,…
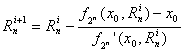 , i=0,1,2,…
, i=0,1,2,…
![]()
![]()
![]()
![]()
![]()
Рассмотрим на примерах как выглядят непосредственные вычислительные формулы.
ПРИМЕР 1: ![]()
![]()
При данном значении функция f будет зависеть только от константы r, обозначим эту функцию как ![]() . Тогда предыдущее уравнение можно будет переписать:
. Тогда предыдущее уравнение можно будет переписать: ![]()
![]()
![]()
ПРИМЕР 2: ![]()
![]()
![]()
![]()
![]()
ПРИМЕР 3: ![]()
![]()
![]()
![]()
![]()
Программу расчета константы ![]() вы можете найти здесь. Её легко модицифировать для расчета постоянной
вы можете найти здесь. Её легко модицифировать для расчета постоянной ![]() , что предоставляется проделать читателю. Результат расчета
, что предоставляется проделать читателю. Результат расчета ![]() в зависимости от шага i приводится ниже.
в зависимости от шага i приводится ниже.
| i |
|
| 1 | 6.9032539091... |
| 2 | 4.7443094689... |
| 3 | 4.6744478277... |
| 4 | 4.6707911502... |
| 5 | 4.6694616483... |
| 6 | 4.6692658098... |
| ... | ... |
| 11 | 4.66920173800930... |
(1) Г.Шустер, "Детерминированный хаос. Введение", М:Мир, 1988
(2) K.Briggs "Feigenbaum Scaling in Discrete Dynamical Systems", PhD thesis, 1997
(3) Е.Б.Вул, Я.Г.Синай, К.М.Ханин, "Универсальность Фейгенбаума и термодинамический формализм", УМН, т.39, вып.3(237), 1984
(4) М.Фейгенбаум, "Универсальность в поведении нелинейных систем", УФН, т.141, вып.2, октябрь 1983
(5) Н.Н.Калиткин, "Численные методы", М:Наука, 1978
(6) Метод Ньютона