Исследование и прогнозирование устойчивости стволов горизонтальных скважин баженовских отложений, бурящихся на депрессии
Владимир Карев, к.ф.-м.н., Юрий Коваленко, к.ф.-м.н., Юрий Кулинич, к.ф.-м.н., Институт проблем механики РАН, НИЦ «Геомеханика и технология»
Расширение объемов бурения горизонтальных скважин (ГС) на депрессии приводит к возникновению целого ряда не существовавших ранее проблем. В частности, обеспечения устойчивости стволов скважин в продуктивных горизонтах и перекрывающих их отложениях при бурении на депрессии.
В статье приведены результаты исследования данной проблемы, выполненного по заказу ОАО «Сургутнефтегаз», применительно к горным породам баженовских отложений из скважин Ульяновского, Сыхтынглорского и Камынского месторождений.
Привлекательность технологии бурения скважин на депрессиях в значительной мере обусловлена возможностью получать минимальное загрязнение призабойной зоны пласта частицами бурового раствора и тем самым сохранять ее природную проницаемость. Вместе с тем при поддержании на забое скважины в ходе ее бурения давления ниже пластового на первый план выходят вопросы, связанные с деформированием и прочностью горных пород, устойчивостью стволов скважин и т.п. Основным вопросом, на который следует ответить перед началом проводки скважины на депрессии, является вопрос о том, на какой максимальной депрессии можно вести бурение. Ответ на этот вопрос зависит от многих факторов — деформационных и прочностных свойств породы, анизотропии ее механических свойств, напряжений, возникающих в окрестности скважины, геометрии скважины, давления на забое скважины.
При ярко выраженной анизотропии прочностных и деформационных свойств породы важнейшим фактором является ориентация скважины относительно осей анизотропии породы. Возможна ситуация, когда при всех прочих одинаковых технологических параметрах (типе бурового раствора, депрессии на забое скважины, скорости проходки и т.д.) бурение на депрессии вертикальных скважин протекает без осложнений, а бурение горизонтальных или наклонных скважин представляет большую проблему в связи с потерей устойчивости.
Чтобы ответить на перечисленные вопросы, недостаточно одних теоретических исследований. Необходимо иметь возможность определять деформационные и прочностные свойства пород для конкретных месторождений и конкретных условий бурения скважин, что можно сделать лишь на соответствующем экспериментальном оборудовании.
Постановка задачи, предварительные измерения и расчеты
Цель работы — определение величины депрессии, при которой возможна потеря устойчивости горизонтальных стволов скважин баженовских отложений в процессе бурения на депрессии. Исследования проводились на уникальной экспериментальной установке Института проблем механики РАН — Испытательной системе трехосного независимого нагружения (ИСТНН), позволяющей на образцах породы размером 5х5х5 см воссоздавать реальные напряжения, возникающие в породе вокруг скважины в процессе ее бурения, освоения и эксплуатации, и исследовать их влияние на фильтрационные свойства породы. В процессе испытаний образцов изучался характер их деформирования, разрушения при моделировании условий роста депрессии на забое скважины. Предварительно были определены скорости распространения продольных волн в исследуемых породах в трех взаимно перпендикулярных направлениях.
В процессе работы на стенде испытаны по различным трехмерным программам нагружения 32 образца породы из продуктивных горизонтов и перекрывающих их отложений.
Как известно, к разрушению материалов приводят касательные (сдвиговые) напряжения. При создании депрессии, например в вертикальной не обсаженной скважине, в породе, слагающей стенки скважины, происходит такое перераспределение напряжений, при котором напряжения, действующие в радиальном направлении на стенке скважины, уменьшаются на величину депрессии, кольцевые (тангенциальные) напряжения увеличиваются, а напряжения, действующие в вертикальном направлении, остаются примерно на том же уровне.
В результате при увеличении депрессии в породе вокруг скважины происходит рост касательных напряжений, что в итоге может привести к ее разрушению. Изменение напряжений в породе вблизи скважины при изменении величины депрессии для различных вариантов конструкции забоя показывают расчеты. В простых случаях (открытый ствол скважины) аналитические, в более сложных (наличие обсадки, перфорационных отверстий, щелей и т.п.) — численные, с использованием трехмерных программ расчета напряженно-деформированного состояния. Найденные условия нагружения породы при изменении величины депрессии для различных вариантов конструкции забоя моделируются на образцах из кернового материала с помощью испытательного стенда ИСТНН.
Для составления программы нагружения образцов, отвечающей реальным напряжениям, возникающим вокруг ГС при создании в ней депрессий различного уровня, необходимо решить две предварительные задачи:
— установить вид анизотропии породы, поскольку от этого в случае горизонтальной скважины во многом зависят действующие вокруг нее напряжения;
— определить упругие модули породы, отвечающие установленному виду анизотропии.
Для определения типа анизотропии породы были измерены скорости распространения продольных волн в изготовленных образцах. Скорости измерялись в трех взаимно-перпендикулярных направлениях: по оси керна и по двум осям в горизонтальной плоскости. Измерения проводились на специальной установке, представляющей собой два датчика-генератора ультразвуковых волн, между которыми устанавливался исследуемый образец. Для визуализации результатов измерений электрические сигналы с обоих датчиков выводились на осциллограф. Между датчиками-генераторами пропускались волны длиной 5 мм, частотой 1,25 МГц и определялось время прохождения волн через образец и затухание амплитуды колебаний.
Скорости распространения продольных волн в горизонтальной плоскости по осям 2 и 3 оказались практически одинаковыми. Скорость распространения продольных волн в вертикальном направлении, т.е. по оси 1, оказалась в 1,2-1,8 раза меньше, чем в горизонтальном.
Полученные результаты позволили сделать вывод, что исследуемая порода, во-первых, является существенно анизотропной и, во-вторых, по своим свойствам близка к трансверсально изотропной среде, т.е. среде, свойства которой в плоскости изотропии (в данном случае в горизонтальной плоскости) одинаковы, а в вертикальном направлении вдоль оси изотропии (оси керна) — отличны.
В ходе измерения скоростей продольных волн был получен еще один интересный результат: коэффициент затухания амплитуды волн в вертикальном направлении был очень большим и превосходил коэффициент затухания амплитуды волн в горизонтальном направлении на порядки. Этот факт свидетельствует о значительной трещиноватости породы в горизонтальном направлении, т.е. порода представляет собой своего рода «слоеный пирог». Об этом же свидетельствует и наблюдавшееся при изготовлении образцов дискование керна при резке его алмазными кругами, поскольку наличие горизонтальной трещиноватости приводит к значительному снижению прочности породы на сдвиг в горизонтальных плоскостях.
Деформирование трансверсально-изотропного упругого материала характеризуется пятью независимыми упругими константами:
— E, E'— модули Юнга в плоскости изотропии и перпендикулярно ей;
— v, v'— коэффициенты Пуассона в плоскости изотропии и перпендикулярно ей;
— G'— модуль сдвига для любой плоскости, перпендикулярной плоскости изотропии.
Для определения упругих свойств породы были специально изготовлены 4 образца — два образца из скв. № 3303 Сыхтынглорского месторождения и два образца из скв. № 3304 Ульяновского месторождения. Особенностью образцов, предназначенных для определения упругих модулей породы, является высокая точность их изготовления: непараллельность противоположных граней образца не превышала 1-2 мкм.
Напряжения и деформации для трансверсально-изотропного материала с учетом расположения осей связаны следующими уравнениями:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() , (6)
, (6)
где:
εi, σi— деформации и нормальные напряжения вдоль i-й оси, i=1,2,3;
ij, ij — деформации сдвига и касательные напряжения в соответствующих плоскостях;
![]() — модуль сдвига для плоскости изотропии.
— модуль сдвига для плоскости изотропии.
Для определения упругих констант каждый образец испытывался по трем программам нагружения. Задавая значения приращений напряжений Δσ и измеряя соответствующие приращения деформаций Δεi , были определены значения упругих модулей Е, Е', v и v'.
Испытания показали, что модули упругости Е' вдоль вертикальной оси для всех образцов примерно в полтора раза ниже, чем модули упругости Е в горизонтальной плоскости, и составляют примерно 1,5-2.105 атм., а коэффициенты Пуассона примерно одинаковы и равны 0,14-0,20.
Более подробно методики измерения скоростей продольных волн в породе и определения ее упругих характеристик будут описаны в статье в одном из следующих номеров журнала.
Что касается пятой упругой константы — модуля G', то для его определения необходимо иметь возможность выпилить образец под углом 45° к оси изотропии, т.е. к оси скважины. Керн диаметром 80 мм, предоставленный для проведения исследований, не позволял этого сделать. Но поскольку величина G' необходима для расчетов, то для ее задания были использованы результаты, приведенные в (1). В ней собраны численные значения всех технических упругих констант для 47 различных горных пород (алевролиты, песчаники, известняки, сланцы и т.д.). Численные значения констант взяты из экспериментальных исследований разных авторов. Анализ этих данных позволил сделать следующий вывод. Хотя модуль G' является независимой константой, для 45 пород (из 47) можно указать приближенную формулу, связывающую G' с остальными упругими константами:
![]() . (7)
. (7)
Поэтому в дальнейшем мы будем пользоваться значениями G', полученными из этой формулы.
Программы испытаний образцов
Одним из основных достоинств испытательного стенда ИСТНН является возможность воссоздания на нем истинных напряженных состояний, возникающих в породе в окрестности скважины, вблизи перфорационных отверстий, щелей и т.д., на любой стадии бурения, освоения и работы скважины.
Это в полной мере относится и к ГС, бурящимся в пластах с ярко выраженной анизотропией деформационных свойств породы. Однако подход к моделированию напряженно-деформированных состояний, возникающих вокруг ГС в трансверсально-изотропном пласте, значительно отличается от того, который обычно применяется для случая вертикальных скважин. Это связано с тем, что в случае вертикальной скважины все точки на ее контуре абсолютно идентичны с точки зрения действующих в них напряжений как для изотропного, так и для трансверсально-изотропного пласта. В горизонтальной же скважине дело обстоит иначе. Если в случае изотропного пласта действующие напряжения также постоянны по контуру скважины, то при наличии анизотропии напряжения существенно меняются по контуру скважины и зависят от упругих характеристик породы.
На рис. 1 схематично показано сечение горизонтальной не обсаженной скважины и действующие на стенках скважины радиальное σR и кольцевое σθ напряжения в двух точках M и N.
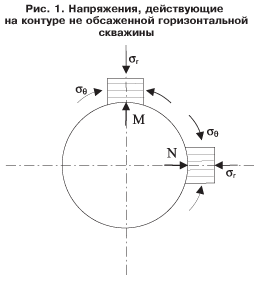
Радиальные напряжения σR во всех точках по контуру скважины одинаковы и равны давлению жидкости в скважине. Кольцевые же напряжения σθ будут меняться от точки к точке.
На рис. 2 показано распределение кольцевых напряжений σθ вокруг горизонтальной скважины в трансверсально-изотропной среде, ось скважины параллельно плоскости изотропии (1). При расчетах в соответствии с измеренными значениями модулей упругости образцов породы в вертикальном и горизонтальном направлениях полагалось, что модуль упругости породы в вертикальном направлении в 1,5 раза меньше модуля упругости в горизонтальном направлении. В качестве единицы на рис. 2 принята разность между величиной горного давления на данной глубине и значением давления жидкости в скважине. Изображенная на рис. 2 окружность представляет собой кольцевые напряжения σθ, которые бы действовали в окрестности горизонтальной скважины, если бы пласт был изотропным. Из рис. 2 видно, что максимальные кольцевые напряжения σθ действуют в точках M и N. Поэтому максимальные касательные напряжения, действующие в окрестности скважины и равные (σθ-σR)/2, также будут наибольшими в этих точках.
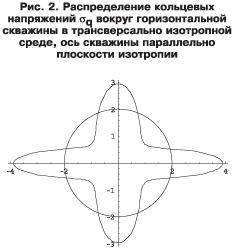
Поскольку разрушение породы происходит за счет действия касательных напряжений, на установке ИСТНН моделировались напряженные состояния именно в точках M и N, как наиболее опасных с точки зрения разрушения ствола скважины. Основное отличие при испытаниях образцов для точек M и N состояло в том, что в точке N напряжения σθ действуют перпендикулярно плоскости напластования, а в точке M — параллельно ей. Соответственно должны располагаться в нагружающем узле ИСТНН и образцы породы во время испытаний.
При уменьшении давления жидкости в скважине радиальные напряжения σR в точках M и N, равные давлению жидкости, будут также уменьшаться, а кольцевые напряжения σθ будут расти, поскольку они пропорциональны разности между величиной горного давления и значением давления жидкости в скважине.
Соответствующая программа испытаний показана на рис. 3. Изображенные на нем напряжения (σ1, σ2, σ3 относятся к осям нагружающего узла ИСТНН, в которых по оси 2 напряжение всегда возрастает, т.е. напряжение σ2 является так называемым параметром нагружения. Применительно к осям скважины напряжение σ2 отвечает напряжению σθ.
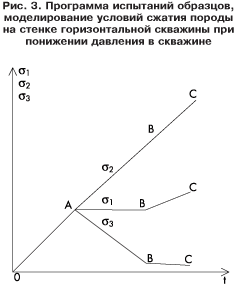
Этап 1. Образец обжимается равномерно со всех сторон до напряжения, равного разности между значением горного давления q и величины начального пластового давления Р0 (отрезок ОА). Точка А отвечает напряжениям, действовавшим в грунтовом скелете до бурения скважины.
Этап 2. На втором этапе нагружения (отрезки АВ) одна компонента напряжения σ2, отвечающая напряжению σθ, продолжает расти, вторая — σ1, соответствующая горному давлению — остается постоянной, а третья — σ3, соответствующая напряжению σR — убывает. Конечная точка этапа (точка В) отвечает состоянию, когда скважина пробурена и заполнена жидкостью.
Этап 3. На третьем этапе моделируется процесс понижения давления в скважине (отрезки ВС). При этом напряжение σ3 остается равным практически нулю, а напряжения σ1 и σ2 растут, но напряжение σ1 растет медленнее. Третий этап является последним и продолжается до тех пор, пока образец не разрушится.
В ходе всего опыта измеряются деформации образца в трех направлениях.
Остановимся подробнее на определении значений напряжений, соответствующих различным точкам программы нагружения образцов. Напряжение σ2, как указывалось выше, отвечает кольцевому напряжению σθ, действующему на контуре скважины. Для горизонтальной не обсаженной скважины, пробуренной в трансверсально-изотропном пласте, это напряжение определяется на основании решения, приведенного в (1). Величина напряжения σθ и характер его изменения по контуру скважины зависят главным образом от упругих модулей породы. Для упругих констант E, E', ν, ν', определенных в результате испытаний, и модуля сдвига G', рассчитанного по формуле (7), как показали расчеты, действующие по контуру скважины напряжения σθ практически совпадают с напряжениями σθ, которые действуют на контуре горизонтальной не обсаженной скважины в изотропном пласте. Таким образом, для определения напряжений σ1, σ2, σ3, отвечающих той или иной величине депрессии в скважине, можно с хорошей точностью использовать известное решение задачи Ламэ. Коротко это решение сводится к следующему.
Напряжения, действующие в грунтовом скелете, равны:
Si = σi + P ,
где:
σi — полные напряжения, обусловленные действием горного давления;
(σi < 0), P — давление нефти (P > 0).
Их значения определяются соотношениями Ламэ:
![]() (8),
(8),
![]()
![]()
где :
q — горное давление (q < 0 ), Рс — давление в скважине, P (r) — давление на расстоянии r от скважины ( Р, Рс > 0 ), Rс — радиус скважины, r — расстояние от оси скважины.
Касательные напряжения = 1/2 (SR — Sθ) равны:
![]() . (9)
. (9)
Из (8) следует, что на стенке скважины, т.е. при r = Rс, напряжения равны:
![]() (10).
(10).
![]()
![]()
Величина депрессии в скважине ΔРс связана с напряжением Sθ, действующим на ее стенке, соотношением:
![]() , (11)
, (11)
где P0 — пластовое давление нефти.
Тогда в программе нагружения, изображенной на рис. 3, характерные точки соответствуют следующим значениям:
в точке А σ1 = σ2 = σ3 = q + Р0 ;
в точке В σ2 = 2 (q+Р0), σ1 = q+Р0, σ3=0, причем среднее напряжение s = (σ1+σ2+σ3)/3 на участке АВ сохранялось постоянным — это следует из соотношений (8);
на участке ВС, моделирующем увеличение депрессии, если образец не разрушался при максимально возможных депрессиях, осуществлялась разгрузка образца, причем точно в обратном порядке по отношению к нагружению образца.
Результаты испытаний образцов
Образцы породы, изготовленные из предоставленного кернового материала, были испытаны на ИСТНН по программе нагружения, описанной выше. При моделировании депрессии в скважине (участок ВС на рис. 3) шаг догружения образцов соответствовал увеличению депрессии в скважине на 25 атм. Часть образцов была испытана при Р0, равном гидростатическому давлению на данной глубине, а остальные образцы — при АВПД, равном 1,4 и 1,7.
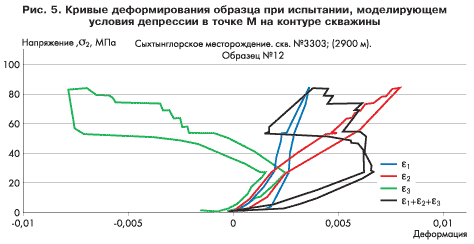
Образцы ориентировались в нагружающем узле ИСТНН двумя способами: ориентация одних образцов соответствовала точке N на рис. 1, а других — точке M. Опыты показали, что образцы, ориентированные согласно точке N, деформировались практически упруго в ходе всего опыта, и их разрушение если и происходило, то лишь при очень больших депрессиях (150-200 атм.). В то же время образцы, ориентированные согласно точке М, зачастую начинали интенсивно деформироваться и разрушаться при низких депрессиях в 10 -25 атм. Яркий пример этому поведение близких образцов № 10 и № 12 скв. 3303 Сыхтынглорского месторождения (рис. 4,5). Образец № 10, ориентированный согласно точке N, практически не «полз» вплоть до создания больших депрессий, а ползучесть образца № 12 началась уже при небольших депрессиях порядка 25 атм.
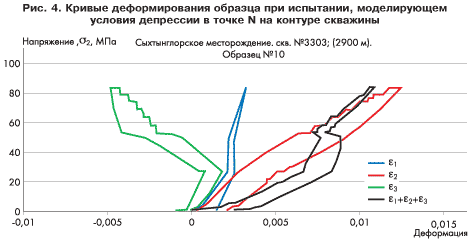
Этому есть ясное физическое объяснение. Дело в том, что исследуемая порода помимо анизотропии по упругим характеристикам обладает также ярко выраженной анизотропией по прочностным свойствам: прочность породы в вертикальном направлении, т.е. перпендикулярно напластованию, в таких средах значительно ниже, чем в горизонтальном направлении, т.е. по напластованию. В точке М порода при понижении давления в скважине разгружается в вертикальном направлении, т.е. а направлении, в котором у нее прочность наименьшая. Кроме того, она при этом подвергается еще большему сжатию вдоль слоев кольцевым напряжением σθ, что также способствует расслоению породы в вертикальном направлении. Именно такой вид разрушения породы и наблюдался в большинстве опытов. В точке N мы имеем иную картину. Порода здесь при понижении давления в скважине разгружается вдоль напластования, т.е. в направлении, в котором прочность породы максимальна. Более того, горизонтальные слои оказываются сжаты большими кольцевыми напряжениями σθ, что также повышает сопротивляемость породы разрушению. В результате вблизи точки N даже при больших депрессиях разрушение породы не наступает.
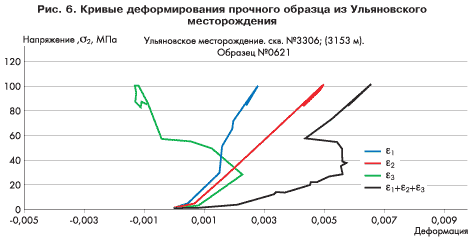
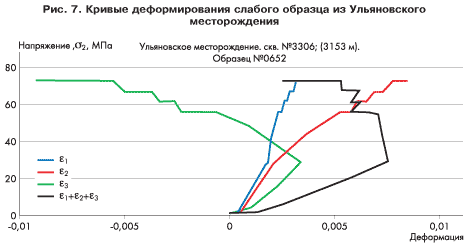
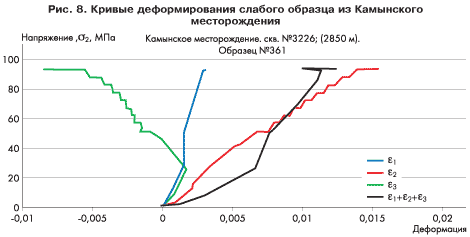
Важнейшей характеристикой для прогнозирования устойчивости стволов скважины при бурении является скорость ползучести породы. Скорость ползучести — это деформация, накапливаемая породой в единицу времени при постоянной нагрузке. Ползучестью в той или иной мере обладают все горные породы, но обычно она бывает столь мала, что не вызывает осложнений при бурении и эксплуатации скважин. Однако есть породы, обладающие сильной ползучестью. В этом случае за достаточно непродолжительное время накапливаемая в породе деформация может достигать критического значения (предельной деформации), при котором начинается разрушение породы. С этой точки зрения все испытанные образцы можно разделить на две группы: примерно половину составили прочные образцы, которые даже под действием напряжений, отвечающих максимальным депрессиям (150-200 атм.), деформировались упруго без всяких признаков разрушения, а половину — слабые образцы, которые начинали интенсивно деформироваться («ползти») и разрушаться уже при низких нагрузках, отвечающих депрессиям 5 — 25 атм. В качестве примера на рис. 6 показаны результаты испытаний прочного образца, а на рис. 7 и рис. 8 — слабых образцов.
Заключение
Результаты испытаний образцов на установке ИСТНН показали, что бурение горизонтальных стволов на депрессии в баженовских отложениях с большой вероятностью может привести к потере устойчивости даже при минимальных депрессиях 5-25 атм.
Этот вывод в наибольшей степени обоснован для Ульяновского месторождения, поскольку для него была испытана достаточно представительная коллекция образцов. Для более обоснованных выводов по Камынскому и Сыхтынглорскому месторождениям требуется проведение дополнительных испытаний.
В ходе испытаний образцов была установлена существенная зависимость прочности породы от направления разгрузки по отношению к направлению плоскостей напластования. С этим явлением, вероятно, связано хорошо известное на практике влияние геометрии ствола скважины на устойчивость пород.
Результаты проведенных исследований позволяют сделать важный вывод о том, что при бурении ГС на депрессиях роль деформационных и прочностных свойств пород, в которых ведется бурение, многократно возрастает по сравнению с обычными технологиями проводки скважин. Без знания таких характеристик пласта, как вид и степень его анизотропии, значение упругих и прочностных констант в разных направлениях, степень деформирования и ползучести породы при различных нагрузках и геометрии скважин невозможно выбирать оптимальные технологические параметры ведения работ, обеспечивающих устойчивость стволов скважин при бурении. Этот вывод в полной мере относится и к бурению наклонных скважин.
1. Лехницкий С.Г. Теория упругости анизотропного тела. М. Изд-во «Наука», 1977, с. 178.