Сплавы магнитных переходных металлов

В последние годы интенсивно изучали электронную структуру и разнообразие физических свойств сплавов переходных металлов. Для изучения магнитных свойств сплавов переходных металлов очень полезным оказался метод рассеяния медленных нейтронов. Исследование упругого и неупругого рассеяния медленных нейтронов в сплавах позволяет получить уникальную информацию о магнитных моментах и форм-факторах, а также об изменении спин-волновой жесткости.

Небходимо отметить, что нейтронные исследования распределения магнитного момента в магнитных сплавах и изменение спин-волновой жесткости во многом стимулировали развитие современных методов расчета электронной структуры неупорядоченных сплавов, которые чрезвычайно полезны для решения многих задач физики твердого тела. К ним относят широко теперь известный метод когерентного потенциала (160).

Модель Хаббарда окозалась очень полезной для описания многих электронных и магнитных свойств сплавов переходных металлов и успешно применяется в большом количестве работ. При описании неупорядоченных сплавов с помощью модели Хаббарда вводятся случайные параметры, поэтому говорят о модели Хаббарда со случайными параметрами.

Перейдем к ее описанию. Предполагается, что взаимодействие электронов в бинарном неупорядоченном сплаве из двух магнитных компонент описывается следующим модельным гамильтонианом:

(69)

Здесь, как и в (11), , - операторы уничтожения и рождения электронов Ванье в узле i со спином σ. Считается, что интегралы перескока одинаковы для обоих сортов атомов А и В, т.е. ; зонная структура чистых компонент А и В в отсутствие кулоновского взаимодействия одинаковая. Величины и - одночастичный потенциал и внутриатомное кулоновское взаимодействие соответственно:

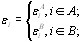
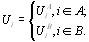(70)

Для неупорядоченного сплава величины и принимают случайные значения в зависимости от того, заполнен ли узел атомом А или В.

Гамильтониан (69) исследовали многие авторы в различных предельных случаях. Если предположим, что какая-либо из компонент сплава (например, В) состоит из немагнитных атомов, то можно положить параметр . Этот случай соответствует модели Вольфа (161, 162). Если положим в (69), получим модельный гамильтониан, который рядом авторов (163, 164) был использован для теоретического описания сплава Pd-Ni. Случай, когда , рассмотрен Лютером и Фульде (165) для анализа рассеяния парамагнонов на примесях; Ямада и Шимицу (166) рассчитали спин-волновой спектр. Мория {167) детально исследовал электронную структуру вблизи магнитной примеси () в немагнитной матрице () и рассчитал целый ряд физических характеристик примесной системы. Взаимодействие между примесями было рассмотрено в (168). Все упомянутые работы (161-168) ограничены приближением сильно разбавленного сплава.

Метод когерентного потенциала (160) позволяет рассматривать сплав с конечной концентрацией примесей. Можно выделить два направления работ, использующих метод когерентного потенциала для описания неупорядоченных сплавов.

Начало первому направлению положила работа (169). В ней была дана теоретическая интерпретация зависимости от концентрации средней намагниченности, атомных моментов компонент и электронной теплоемкости для сплава NicFe1-c. К этому направлению примыкают работы (170-174).

Подход Хасегава и Канамори (ХК) основан на использовании приближения Хартри-Фока для описания внутриатомной кулоновской корреляции. В этом случае гамильтониан (69) записывался в следующем виде (169):

(71)

где

(71а)

таким образом, неупорядоченность, описываемая в рамках приближения когерентного потенциала, характеризуется двумя параметрами и . Средние числа заполнения в (71а), которые различаются для разных компонент сплава ( или , i∈A, или В), должно определяться самосогласованным образом. Последнее обстоятельство приводит к тому, что не каждая элементарная ячейка является электрононейтральной и может иметь место перенос конечного заряда.

Для одночастичного гамильтониана (71) применима стандартная схема метода когерентного потенциала, которую здесь опишем, следуя обозначениям работы (160). В методе когерентного потенциала (СРА) рассматривается одноэлектронный гамильтониан следующего вида:

(72)

Здесь W – периодическая часть; D – сумма случайных вкладов, каждый из которых связан с одним узлом. Одноэлектронные свойства сплава вычисляются как средние по ансамблю по всем возможным конфигурациям атомов в решетке. Обычно рассматривают усредненную подобным образом одноэлектронную функцию Грина G(z):

(73)

Определим Т-матрицу для данной конфигурации сплава с помощью уравнения

(74)

Тогда функциональное уравнение для определения неизвестного оператора Σ будет задаваться условием

(75)

Уравнение (75) является самосогласованным определением оператора Σ.

Полагая, что

(76)

можно ввести локальный оператор рассеяния

(77)

С помощью оператора Tn эффективная среда, характеризуемая оператором Σ, заменяется рассеянием на реальном атоме в данном узле n. В методе когерентного потенциала общее условие самосогласования (75) заменяется его одноузельным приближением

(78)

таким образом, при этом подходе примесь считается находящейся в эффективной среде, функция Грина которой подбирается так, чтобы Т-матрица рассеяния на примеси в среднем была равна нулю. При этом будем пренебрегать рассеянием парами атомов и более крупными кластерами. Метод когерентного потенциала точен в атомном пределе, когда перескоки электронов с узла на узел очень маловероятны. Сравнение приближений виртуального кристалла, средней Т-матрицы и когерентного потенциала, проведенное в (175), показало, что метод когерентного потенциала не хуже аппроксимации виртуального кристалла.

В методе когерентного потенциала усредненная функция Грина неупорядоченной системы получается из функции Грина для идеальной решетки заменой энергии на комплексную величину. Аналитические свойства величин, вычисляемых в одноузельном приближении когерентного потенциала, нетривиальны; функция Грина аналитична всюду, кроме линий разрезов, соответствующих примесной зоне и зоне основного кристалла.

Существенно, что в методе когерентного потенциала эффект рассеяния электронов вследствие неупорядоченности описывается комплексной величиной, а именно когерентным потенциалом. С точки зрения квантовой механики в этом нет ничего необычного. Напомним, что при многократном рассеянии волны на произвольном ансамбле рассеивателей вводится усредненная по ансамблю волновая функция, а потенциал в уравнении Шредингера становится комплексным (176). Мнимая часть потенциала описывает поглощение вследствие рассеяния.

Основная характеристика спектра возбуждений системы есть плотность состояний на единицу энергии D(ε). Она определяется мнимой частью функции Грина =GCPA. На основе одночастичной плотности состояний с помощью метода когерентного потенциала можно хорошо описать поведение параметра асферичности γ для сплавов Ni, Fe и Co (177).

Параметр асферичности является важной характеристикой, экспериментально измеряемой с помощью рассеяния медленных нейтронов и определяется следующим соотношением:

g/ μ (79)

где μ eg - магнитный элемент, определяемый электронами в состояниях eg- типа, μ - полный спиновый магнитный момент.

Эксперименты по рассеянию нейтронов показывают, что измеряемые значения γ в зависимости от μ очень точно укладываются на прямую линию практически для всех сплавов Ni, Fe и Co. Т. е.

γ = а +bμ (80)

Только для чистого Ni это не выполняется; γNi значительно меньше величины, следующей из (80). Возможной причиной такого отклонения для чистого Ni может быть либо влияние корреляции электронов, либо специфика одно-частичного поведения системы. В (177) были рассмотрены только одно-частичные свойства системы в подходе Хасегава и Канамори (71) и показано, что для расчета параметра асферичности влияние корреляции не очень существенно. Как и в (169), рассматривалась область концентраций сплава при 0 ≤ с ≤ 0,5. Хасегава и Канамори с помощью метода когерентного потенциала вычислили магнитный момент μ и локальные моменты μ (Ni) и μ (Fe). Их результаты хорошо согласуются с экспериментом. Однако, надо заметить, что они использовали не реальную плотность состояний, а сильно идеализированную функцию и проблема решалась с использованием многих свободных параметров.

В (177) впервые была использована реальная теоретическая плотность состояний (51, 178) для расчета параметра асферичности γ Для точного расчета γ необходимо было отдельно учесть eg- и t2g – состояния. Получить такие раздельные плотности весьма сложно из-за сильной гибридизации этих состояний. В (177) использовано то обстоятельство, что в точках и на линиях высокой симметрии, где гибридизация отсутствует, волновые функции можно отождествить с eg- и t2g – состояниями. Предполагалось, что количественно поведение волновых функций не сильно изменяется при переходе к другим точкам. Используемая теоретическая плотность состояний состоит из шести подзон, две из них связаны с s-электронами, а остальные четыре имеют в указанных точках и на линиях высокой симметрии поведение плотности состояний электронов в t2g и eg-состояниях. Поэтому можно предположить приближённое разделение плотности состояний на составляющие для t2g и eg- – электронов.

В методе когерентного потенциала, выражение для плотности состояний в сплаве имеет вид (177)

(ε) = - Im (ε), (81)

где

=; (82)

Σi – когерентный потенциал, определяемый из уравнения

Σi = х Δ + Σi (Δ - Σi ) (ε) (83)

Δ описывает сдвиг между атомными уровнями Fe b Ni. В (169) этот параметр очень сильно зависит от спина (Δ/Δ=5,6) и от концентрации. В (177), напротив, предполагалось, что Δ практически не зависит от этих величин, чтобы последовательно провести учёт одно-частичных свойств модели. Решение задачи удаётся провести без использования свободных параметров. Были вычислены плотность состояний (ε) и локальные плотности и для i = t2g и различных концентраций. Полученный на основе этих результатов для параметр асферичности γ показан на рис. 11. согласие с экпериментом хорошее.

Интересно отметить, что результаты для вычисленных Эльком значений μ, μ(Ni) и μ (Fe) оказываются хуже, чем в работе Хасегава и Канамори. Возможной причиной этого может быть влияние корреляций на значение μ, для описания которой в (169) использовали дополнительные свободные параметры. В то же время, как видно на рисунке 11 поведение параметра асферичности хорошо объясняется уже на основе одно-частичной плотности состояний оптимально приближённой к реальной. Дальнейшее обсуждение подхода Хасагава –Канамори дано в (179).

Другое направление описания неупорядоченных сплавов с помощью гамильтониана (69) развивалось в (180-181); конкретно (180) рассматривался сплав Pd-Ni. Подробно проанализировал различие этих двух подходов Фукуяма. (162, 174). Он показал, что в подходе Харриса-Цукермана (180) основное внимание сосредотачивается на динамических эффектах кулоновского взаимодействия, а пространственным изменением потенциала пренебрегается. Поэтому такие одно-частичные величины, как локальная плотность состояний, являются пространственно однородными, за исключением возможного существования виртуально связанных состояний. Схема является самосогласованной, если имеет место равенство ….. в управлении (69); в этом случае возможно, в отличие от (71) учесть некоторые процессы элекрон-дырочного рассеяния более высокого порядка.

Различие между подходами Хосегава-Канамори (169, 173, 179) и Харриса-Цукермана (180) наиболее заметно проявляется при рассмотрении коллективных эффектов, в частности, при вычислении спиновой восприимчивости. Это связанно с тем, что при построении теории электронных и магнитных свойств неупорядоченных сплавов описывающихся гамильтонианом (69), необходимо учитывать случайное расположение атомов компонент на решётке и влияния кулоновской корреляции электронов на электронную структуру и физические свойства. Если, как мы видели выше, одно-частичные характеристики сплавов (например, параметр асферичности γ ) слабо зависит от корреляционных эффектов. То, для коллективных свойств правильный учёт корреляции более существен.