Поляризация света

ИНСТИТУТ ФИЗИЧЕСКИХ ИССЛЕДОВАНИЙ

Реферат

Поляризация света.

Автор: Осипян Д.С.

АШТАРАК 1999

Введение

Уравнения Максвелла. При наличии электрических зарядов в пространстве устанавливается возбужденное состояние, которое называют электромагнитным полем. Его представляют векторами E и B, именуемыми соответственно электрическим вектором и магнитной индукцией. Для описания влияния поля на материальные объекты необходимо ввести вторую группу векторов, а именно плотность электрического тока J, электрическое смещение D и магнитный вектор H. Пространственные и временные производные пяти указанных векторов связаны уравнением Максвелла.

rot H = J+ D (1)

rot E= - B (2)

div B= 0 (3)

div D = 4 (4)

J =E (5)

D =E (6)

B =H (7)

Величина называется удельной проводимостью, - диэлектрической проницаемостью, а - магнитной проницаемостью.

Волноное уравнение. Рассмотрим случай области поля, не содержащей ни зарядов, ни тонов т.е. . Дифференциальные уравнения, которым должны удовлетворять каждый из векторов в отдельности, можно получить путем исключения остальных векторов. Для однородной среды получим

E - E = 0 (8)

H - H = 0 (9).

Это обычные уравнения волнового движения. Они означают, что существует электромагнитная волна, распространяющаяся со скоростью

v = (10).

Поперечность световой волны. Из электромагнитной теории света вытекает непосредственно, что световая волна поперечна. Вся совокупность законов электромагнетизма и электромагнитной индукции краткое математическое выражение которой заключается в уравнениях теории Максвелла, приводят к выводу, что изменение во времени электрической напряженности E сопровождается появлением переменного магнитного поля H, направленного перпендикулярно к вектору E, и обратно. Такое переменное электромагнитное поле распространяется со скоростью света вдоль линии, перпендикулярной векторам E и H, образуя электромагнитные, в частности световые, нолны. Т.о. , три вектора E, H и скорость распространения волнового фронта v взаимно перпендикулярны и составляют правовинтовую систему; т.е. электромагнитная волна поперечна.

Поляризация света.

Естественный и поляризованный свет. Естественный свет есть совокупность световых волн со всеми возможными направлениями колебаний, быстро и беспорядочно сменяющими друг друга.

Линейно- или плоскополяризованный свет представляет собой световые волны с одним-единственным направлением колебаний ( единственный крест E и H ), т.е. волны с вполне упорядоченным направлением колебаний. Существуют и более сложные виды упорядоченных колебаний, которым соответствуют иные типы поляризаций, например круговая или эллиптическая поляризации, при которых конец электрического ( и магнитного) вектора описывает круг или эллипс с тем или иным эксцентриситетом.

Частично поляризованный свет характеризуется тем, что одно из направлений колебаний оказывается преимущественным, но не исключительным.

Распространение света через турмалин. Вырежем из кристалла турмалина пластинку, плоскость которой параллельна одному из определенных направлений кристаллической решетки, называемой осью , и направим сквозь пластинку свет перпендикулярно к поверхности пластинки. Опыт показывает , что турмалин превращает естественный свет в линейно-поляризованный, задерживая половину его, соответствующую той слагающей электрического вектора, которая перпендикулярна к оси кристалла, так что за кристаллом окажутся волны, направление электрического вектора которых параллельно оси кристалла. Кристалл , т.о. , выделяет из света со всевозможными ориентациями Е ту часть, которая соответствует одному определенному направлению E.

Поляризация при отражении и преломлении света на границе двух диэлектриков. Явление поляризации света , т.е. выделения световых волн с определенной ориентацией электрического ( и магнитного ) вектора имеет место и при отражении или преломлении света на границе двух изотропных диелектриков.

Пусть параллельный пучок естественного света падает на стеклянное зеркало. Отраженный свет исследуется при помощи турмалина. Поляризация света, отраженного от диэлектрика, оказывается частичной. При изменении угла наклона зеркала к лучу изменяется доля поляризованного света . При определенном значении угла (угол Брюстера) отраженный свет оказывается полностью поляризованным. Величина этого угла полной поляризации зависит от относительного показателя преломления n и определяется, как установил Брюстер, соотношением

tg=n (11).

Исследование показывает, что электрический вектор в отраженном свете в случае полной поляризации колеблется перпендикулярно к плоскости падения.

Преломленный свет также частично поляризован и притом так, что колебания происходят преимущественно в плоскости падения. При падении под углом Брюстера поляризация преломленных лучей максимальная, но далеко не полная (для обычного стекла она составляет около 15%).

Двойное лучепреломление и поляризация при прохождении через кристалл исландского шпата. Если на кристалл исландского шпата () падает узкий пучок света, то, преломляясь, он дает два пучка несколько различного направления. Если падающий пучок достаточно узок, а кристалл достаточно толст, то из него выходят два пучка, параллельных первоначальному и вполне разделенных пространственно. Один из лучей называют обыкновенным (о), а другой – необыкновенным (е).

В кристалле исландского шпата существует одно направление , вдоль которого оба преломленных луча распространяются не раздваиваясь и с одной скоростью. Направление это принято называть оптической осью кристалла. Плоскость , проходящая через оптическую ось и волновую нормаль распространяющихся волн, носит название главной плоскости.

Пусть световой пучок нормально падает на естественную грань кристалла. Из кристалла выйдут два луча , лежащие в главной плоскости и параллельных падающему. Оба луча вполне поляризованны во взаимоперпендикулярных направлениях. Колебания вектора обыкновенной волны проходят перпендикулярно к главной плоскости, а необыкновенной – в главной плоскости.

Эллиптическая и круговая поляризация света. Рассмотрим результат сложения двух когерентных световых волн, поляризованных в двух взаимно перпендикулярных направлениях, имеющих разную амплитуду и обладающих некоторой разностью фаз. Мы легко можем осуществить подобный случай на опыте. Свет определенной длины волны , прошедшей через поляризатор, пропустим через кристаллическую пластинку толщины d , вырезанную из одноосного кристалла параллельно его оптической оси (рис 1) , причем допустим, что направление пучка перпендикулярно к боковой поверхности пластинки.

Рис. 1.

Сквозь пластинку будут распространяться в одном направлении, но с разной скоростью две волны, поляризованные в двух взаимоперпендикулярных направлениях, которые принято называть главными направлениями кристаллической пластинки. У одной из волн электрические колебания направленны вдоль оптической оси кристалла, например по CC ( необыкновенный луч, показатель преломления ) , у другой – перпендикулярно к оси , т.е. по BB ( обыкновенный луч, показатель преломления ).

Если направление колебаний электрического вектора в падающем поляризованном свете составляет угол a с одним из главных направлений пластинки, то амплитуды колебаний в необыкновенной и в обыкновенной волнах будут соответственно равны

,

где - амплитуда падающей волны. Пройдя через через толщу пластинки , эти две волны приобретут разность хода , равную . Следовательно, обыкновенная волна отстает по фазе от необыкновенной на на величину

(12)

Сложение двух взаимно перпендикулярных колебаний с разными амплитудами и разностью фаз приведет к формированию эллиптического колебания, т.е. колебания, при котором конец результирующего вектора описывает эллипс в плоскости волнового фронта с той же угловой частотой , с которой совершаются исходные колебания.

Действительно, колебания в волнах, прошедших пластинку, описиваются соотношениями

(13)

Исключая из этих уравнений получим

, (14)

т.е. уравнение эллипса . Форма эллипса и ориентация его относительно осей и зависят от значений и .

Т.о. получилаем световую волну, концы векторов E и H которой описывают эллипсы. Такой свет называется эллиптически- поляризованным.

Рассмотрим несколько частных случаев.

а) Толщина пластинки такова , что разность хода двух волн составляет четверть длины световой волны (пластинка в ј волны):

или

m=0,1,2. … (15)

В таком случае и уравнение эллипса примет вид

т.е. мы получим эллипс , ориентированный относительно главных осей пластинки. При = находим , так что эллипс обращается в круг, описиваемый уравнением

. (16)

В данном случае имеем свет, поляризованный по кругу (круговая, или циркулярная поляризация).

В зависимости от ориентации пластинки в четверть волны приобретаемая разность фаз равна или , т.е. компонента вдоль оси Ox опережает или отстает на по фазе от компоненты по оси Oy . В соответствии с этим результирующий вектор вращается против часовой стрелки (влево) или по часовой стрелке (вправо). Поэтому принято различать левую и правую эллиптическую или круговую поляризации.

б) Пластинка такова, что разность хода двух лучей составляет половину длины световой волн (пластинка в Ѕ волныи):

или

, (17)

т.е.

или . (18)

, (19)

т.е. свет остается линейно- поляризованным, но направление, но направление колебаний поворачивается на угол .

в) Пластинка в целую длину световой волны (пластинка в ):

или

т.е. или . (20)

, (21)

т.е. луч остается линейно- поляризованным без изменения направления колебаний.

Все предшествующие рассуждения относились к свету определенной длины волны, т.е. к небольшому спектральному интервалу. При значительном разнообразии б длинах волн следует принять во внимание, что показатели преломлений для обоих волн зависит от длины волны (дисперсия), причем их разность также меняется с длиной волны.

Характеристики состояния поляризации с помощью параметров Стокса.Для характеристики эллипса поляризации необходимы три независимые величины, например амплитуды a и b и разность фаз δ или малая и большая оси и угол характеризующий ориентацию эллипса. Для практических целей состояние поляризации удобно охарактеризовать некоторыми параметрами, обладающими одинаковой физической размерностью; они были введены Стоксом.

Параметрами Стокса для плоской монохроматической волны служат четыре величины:

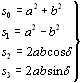(21)

Лишь три из них независимы , т.к. справедливо тождество

(22)

Очевидно, что параметр пропорционален интенсивности волны. Параметры и простым образом связаны с углом характеризующим ориентацию эллипса , и углом , характеризующем эллиптичность и направление вращения. Выполняются следующие соотношения:

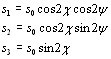(23)

Выражения (23) указывают простое геометрическое представление различных состояний поляризации: и можно рассматривать как декартовы координаты точки P на сфере радиуса , причем и являются сферическими угловыми координатами этой точки. Т.о. , каждому возможному состоянию поляризации плоской монохроматической волны заданной интенсивности ( = const) соответствует одна точка на сфере и наоборот. Т.к. угол положителен или отрицателен в зависимости от того, имеем ли мы дело с правой или с левой поляризацией, то из (23) следует, что правая поляризация представляется точками на , лежащими выше экваториальной плоскости (плоскости xy ), а левая - точками на , лежащими ниже этой плоскости. Далее, для линейно поляризованного света разность фаз равна нулю или целому кратному ; согласно (21) параметр Стокса равен тогда нулю , так что линейная поляризация представляется точками на экваториальной плоскости. Для круговой поляризации и или в соответствии с тем, имеем ли мы дело с правой или левой поляризацией. Следовательно, правая круговая поляризация представляется северным полюсом (), а левая - южным полюсом (). Такое геометрическое представление различных состояний поляризации точками на сфере было предложено Пуанкаре. Оно чрезвычайно полезно в кристаллооптике для определения влияния кристаллических сред на состояние поляризации проходящего через них света. Сфера называется сферой Пуанкаре .