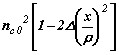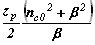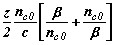Оптические волноводы
Введение
В конце 70-х начале 80-х годов в мире произошёл информационный бум. С начала информацию передавали по проводным линиям связи (попросту говоря по средствам электрических импульсов). Но с передачей сигнала по проводам возникали множественные проблемы да и качество связи желала лучшего. Свет же позволил человеку повысить скорость передачи информации, да и влияний на него меньше. Человек научился использовать свет, направлять его куда это ему необходимо. Это происходит по средствам оптических волноводов, которые имеют неоднородный коэффициент преломления. За счёт этой неоднородности и происходит направление луча свет в нужное “русло”. В данной работе рассматривается принципы и законы, по которым распространяется свет в оптических волокнах, на примере планарного волновода.
Оптические волноводы - это диэлектрические структуры, по которым может распространяться электромагнитная энергия в видимой и инфракрасной областях спектра. Реальные волноводы, используемые в оптической связи, представляют собой гибкие волокна из прочных диэлектрических материалов. Поперечное сечение таких волоконных световодов имеет размеры, сравнимые с размерами человеческого волоса. Обычно состоит из трёх областей: центральная область - сердцевина - окружена оболочкой, которая, в свою очередь, окружена защитным покрытием. Показатель преломления сердцевины n может быть постоянным или изменяться по сечению (зависимо от профиля волновода), показатель преломления оболочки обычно постоянен по сечению. Два случая, соответствуют ступенчатому и градиентному профилям показателя преломления. Чтобы волновод имел направляющие свойства необходимо, чтобы показатель преломления сердцевины хотя бы в части сечения превосходил показатель преломления оболочки. В основном вся энергия (информация) передаётся по сердцевине и лишь её малая часть - по оболочке. Покрытие полностью оптически изолировано от сердцевины, поэтому мы пренебрежём её влиянием и при анализе предположим, что оболочка снаружи не ограничена.
Оптические волноводы можно условно разделить на две группы - многомодовые (с относительно большим поперечным размером сердцевины) и одномодовые (с относительно малым поперечным размером сердцевины). Для многомодовых волноводов справедливо условие ![]() , где ρ - характерный размер сердцевины, например радиус сердцевины волоконного световода, λ - длина волны света в свободном пространстве, nc0 - максимальное значение показателя преломления сердцевины, а nc1 - показатель преломления оболочки.
, где ρ - характерный размер сердцевины, например радиус сердцевины волоконного световода, λ - длина волны света в свободном пространстве, nc0 - максимальное значение показателя преломления сердцевины, а nc1 - показатель преломления оболочки.
Распространение электромагнитных волн по оптическим волноводам может быть описано строго с помощью уравнений Максвелла. Однако хорошо известно, что классическая геометрическая оптика даёт приближённое описание распространения света в среде, где показатель преломления слабо изменяется на расстояниях порядка длины волны света. Это условие обычно выполняется для многомодовых оптических волноводов, используемых в системах связи. Таким образом, наиболее прямой и наглядный способ описания распространения света в многомодовых волноводах - с помощью лучей, распространяющихся по сердцевине.
Краткий теоретический курс.
1. Планарные волноводы.
Типичные представители планарных волноводов состоят из световедущего слоя - сердцевины - толщиной 2ρ, располагающегося между двумя слоями оболочки. Как уже говорилось раньше, для простоты предлагаю, что слои оболочки имеют бесконечную толщину. Плоскости x=±ρ являются границами раздела сердцевина-оболочка. Так как волновод простирается неограниченно во всех направлениях, ортогональных к оси x, то структура является двумерной. Ось z расположена вдоль средней линии между границами разделов и является за чистую осью симметрии. Тогда показатель преломления n(x) в сердцевине может быть либо постоянным по сечению, либо изменяющимся в поперечном направлении. В оболочке, как правило, показатель преломления постоянен по сечению и равен nc1. При этом показатель преломления сердцевины должен превосходить nc1 для обеспечения направляющих свойство волновода. Предположим, что профиль не изменяется вдоль оси z, то есть волновод обладает трансляционной инвариантностью. Параметры представленного волновода и длина волны света λ в свободном пространстве могут быть объединены в один безразмерный параметр V, называемый волновым параметров, или волноводной частотой. Пусть nc0 - максимальное значение n(x) на оси волновода, тогда V определяется следующим образом:
| (1.1) |
2. Построение лучевой траектории.
Траектория луча определяется лучевым уравнением с функцией профиля n(r)
| (2.1) |
где s - расстояние, отсчитываемое вдоль траектории луча, r - радиус-вектор точки на ней. В случаи планарного волновода профиль показателя преломления n(x) зависит только от координаты x, поэтому каждая точка (x,z), составляющая лучевую траекторию определяется с помощью двух (x-го и z-го) компонент уравнения (2.1):
| (2.2) |
Угол θz(х), образующийся между касательной к траектории луча и осью волновода, имеет определённый физический смысл (см. рис. 1).
| (2.3) |
Проинтегрировав второе уравнение (2.2) получим соотношение:
| (2.4) |
справедливое при всех х. Оно является обобщением закона Снелля (приложение 1) для градиентных сред. При этом n(x)cosθz(х) постоянно вдоль траектории луча. Для конкретного профиля траектория луча однозначно определяется начальным углом θz (0).
Каустика точек поворота. Заметим, что если п(х) уменьшается при удалении от оси волновода, то из уравнения (2.4) следует, что внутри сердцевины существует граница, на которой θz(х)=0. Причем положение этой границы определяется значением θz(0). За данной границей распространение луча не возможно. Указанная граница называется точкой поворота xtp которая определяется из условия
| (2.5) |
Сопоставляя понятия кривизны лучевой траектории с понятием точки поворота видно, что траектория луча подобна траектории на рис. 2,а, если уравнение (2.5) имеет разрешимо, и траектории на рис. 2,б, если оно решения не имеет. В первом случае луч непрерывно поворачивается и возвращается к оси, во втором случае луч достигает границы сердцевины и, преломляясь, выходит наружу. Так как профиль непрерывен вблизи границы раздела, то угол падения равен углу преломления, θt=θz(ρ). Штриховая линия, соответствующая х=хtp, представляет собой геометрическое место расположения точек поворота для всех лучей с одинаковым значением θz(0), которое часто называют лучевой каустикой, или каустикой точек поворота.
Характеристики траектории луча. Когда уравнение (2.5) имеет решение луч возвращается к оси z под тем же углом, а то есть, имеет периодический характер. И если профиль показателя преломления симметричный, то есть п(-х)=п(х). То траекторию луча в волноводе можно построить простым повторением отрезков траектории, изображенной на рис. 2,а. И тогда траектория имеет вид синусоиды (рис. 3). Она никогда не достигает границы раздела сердцевина-оболочка, что исключает потери мощности. Такие лучи являются направляемыми. Лучи, траектории которого достигает границы раздела, теряют свою мощность и называются рефрагирующим. Траектория луча, касающаяся границы раздела сердцевины с оболочкой, разделяет области, заполненные траекториями лучей каждого из указанных типов. Для данной граничной траектории хtp=ρ. Обозначая соответствующее этой траектории значение θz(0) через θc(0), из (2.5) получаем
| (2.6) |
предполагая, что n(0)=nc0 - максимальное значение п(х).
направляемые лучи: | (2.7,а) |
рефрагирующие лучи: | (2.7,б) |
Решение уравнения (2.2) для лучевых траекторий рассматривается в разд. 4.
3. Лучевой инвариант.
Следствием трансляционной инвариантности волновода является периодический характер лучевой траектории (рис.3), что позволяет ввести лучевой инвариант β, который постоянен вдоль пути распространения луча и характеризует его направление в любой точке поперечного сечения сердцевины. В волноводе градиентного профиля с учетом (2.3) и (2.4) он определяется следующим выражением:
| (3.1) |
Следовательно, β постоянен вдоль траектории и определяет направление луча в любой ее точке, а также положение точки поворота хtp. Так как в точке поворота θz(х) = 0, то
n(xtp)= β, | (3.2) |
и между хtp и β существует взаимно однозначное соответствие. Классификация лучей в соответствии с (2.7) может быть проведена также и относительно β. При х=0 и θz(0) = θс(0) из уравнения (3.1) с учетом (2.6) следует, что β=nс1. Таким образом,
направляемые лучи: |
| (3.3а) |
рефрагирующие лучи: |
| (3.3б) |
где и nc0 - максимальное значение п(х).
4. Лучевые параметры.
Удобно ввести параметры, характеризующие распространение луча в волноводе с градиентным профилем, которые будут использованы в последующих разделах. К ним относятся, в частности, LP-длина пути (путь между ближайшими точками поворота), L0-оптическая длинна пути (для определения времени прохождения луча, которая определяется как произведение длины пути на показатель преломления) и ZP-полупериод траектории луча, которые легко обобщаются на волноводы с градиентным профилем. Хотя процесс обобщения можно упростить, получив предварительно явное решение систем уравнений (2.2) для траектории луча, однако на практике очень редко используют зависимость характеристик луча вдоль траектории. Заменяя в первом уравнении (2.2) ds на dz из (3.1), после соответствующих преобразований получаем
| (4.1) |
Полагая 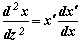 , где
, где![]()
![]() , после интегрирования имеем
, после интегрирования имеем
| (4.2) |
так как ![]() и п(х)=β при х=хtp. Второе интегрирование дает
и п(х)=β при х=хtp. Второе интегрирование дает
| (4.3) |
где z=0 при х=0. Это выражение является точным для траектории направляемых лучей при ![]() и для рефрагирующих лучей при
и для рефрагирующих лучей при ![]() .
.
Параметры траектории луча находятся с помощью рис. 4, на котором представлен отрезок траектории направляемого луча между следующими друг за другом точками поворота Р и Q, отстоящими на расстоянии, равном полупериоду ZP и измеренном вдоль оси волновода. Длина пути L0 и оптическая длина пути LP определяются интегралами по траектории:
| (4.4) |
где s - расстояние вдоль траектории. Заменяя ds на dz из (3.1) и dz на dx из (4.2), получаем
| (4.5) |
Полупериод траектории луча можно получить из (4.3) в виде
| (4.6) |
Следовательно можно определить и количество точек поворота траектории луча на единицу длины волновода ![]() . В случае симметричного профиля интеграл вычисляется для
. В случае симметричного профиля интеграл вычисляется для ![]() , а результат удваивается.
, а результат удваивается.
Локальный критический угол скольжения. Для наглядности в случае рассмотрения волноводов с градиентным профилем удобно ввести дополнительный параметр. В разд. 2 отмечалось, что в любой точке поперечного сечения сердцевины волновода все направляемые лучи распространяются под углами к оси волновода, значения которых лежат в интервале 0=θz<θc, где θc - критический угол скольжения. Однако для волноводов с градиентным профилем область значений углов θz(х) направляемых лучей изменяется в зависимости от положения луча в поперечном сечении. На оси указанная область определяется (2.7а), а на границе сердцевины направляемых лучей нет (Точнее говоря, на границе сердцевины все направляемые лучи имеют θc(x)=0, то есть они параллельны оси волновода). Соответственно определим локальный критический угол скольжения θc(х), как
| (4.7) |
В результате интервал углов направляемых лучей в точке с координатой х определяется следующим образом:
| (4.8) |
При х=0 (4.8) сводится к (2.7а), а при х=ρ θz(х)=0. Все указанные выше параметры, а также время прохождения луча, рассматриваемое в следующем разделе, представлены в приложении 2.
5. Время прохождения луча.
Время прохождения луча в волноводах с градиентным профилем определяется интегралом вдоль искривленной траектории луча (см. рис. 3). Локальная скорость света непрерывно изменяется по закону c/п(х), где с - скорость света в свободном пространстве и п(х) - профиль показателя преломления. Следовательно, время прохождения луча на расстояние z вдоль оси волновода определяется интегральным выражением
| (5.1) |
Оно получено с помощью уравнения (3.1). Здесь интегрирование выполняется вдоль кривой х=х(z). Этот интеграл не имеет простого представления, но его можно аппроксимировать. Из (4.4) следует, что время прохождения луча на расстояние, равное полупериоду траектории zp, и составляет ![]() , где L0 - оптическая длина пути. Таким образом, если z точно кратно полупериоду траектории, то время прохождения луча можно представить выражением
, где L0 - оптическая длина пути. Таким образом, если z точно кратно полупериоду траектории, то время прохождения луча можно представить выражением
| (5.2) |
В общем случае z не кратно zp, однако при z>>zp выражение (5.2) может служить достаточно точным приближением для (5.1).
Выравнивание времени прохождения. В волноводах с градиентным профилем происходит выравнивание времени прохождения для различных лучей, что легко объяснить. Так как п(х) уменьшается при удалении от оси, то чем дальше от оси распространяется луч, тем больше локальная скорость света с/п(х). Такое увеличение скорости частично компенсирует увеличение длины пути неосевых лучей.
6. Параксиальное приближение.
Оптические волноводы, используемые в технике связи, обычно являются слабонаправляющими, то есть перепад между максимумом и минимумом показателя преломления в поперечном сечении мал и обычно не превосходит 1% от максимального значения. Рассмотрим некоторые особенности такого приближения применительно к лучевому анализу.
Если максимальное и минимальное значения показателя преломления близки, то из (2.6) следует, что критические углы скольжения θс и θс(0) малы и справедливо следующее соотношение:
| (6.1) |
аналогичное соотношение получается для θс(0). Таким образом, интервал углов направляемых лучей в (2.7а) мал, и любой направляемый луч распространяется почти параллельно оси. Такое приближение называется параксиальным.
Параксиальное приближение не приводит к упрощению уравнений (2.2), поскольку, как видно из (4.3), β - константа, а п(х) принимает значения, уменьшающиеся вплоть до β. Однако оно позволяет упростить выражения для длины пути zp в (4.5) при использовании указанной ниже аппроксимации. Профиль может быть описан следующим образом:
| (6.2) |
где и nc0 - максимальное значение показателя преломления, f(x)-неотрицательная функция, а Δ -константа, определяемая с учетом (2.6) соотношением
| (6.3) |
В однородной оболочке п(х)=пc1, а f(х)=1. Такое определение Δ предполагает выполнение условия Δ<<1 в приближении слабонаправляющего волновода, то есть условия nc0пc1. Таким образом, в низшем порядке приближения величина Δ представляет собой относительный перепад между пc0 и nc1
| (6.4) |
и характеризует относительную высоту профиля, поэтому параметр Δ будем называть параметром высоты профиля. При Δf(x)<<1 из (6.2) получаем приближенное соотношение
| (6.5) |
которое будет использовано при определении LP ниже.
7. Параболический профиль.
Рассмотрим бесконечный параболический профиль, соответствующий на рис. 5 сплошной кривой q=2 и пунктирному продолжению, который определяется выражением
| (7.1) |
где ρ - эффективная ширина профиля. С одной стороны, показатель преломления непрерывно изменяется в бесконечных пределах (профиль является нереальным), так как ![]() при
при ![]() . Но так как этот профиль является одним из простейших для понимания процессов распространения, мы будем его использовать как составной элемент при анализе волноводов параболического профиля с однородной оболочкой. Так как профиль является бесконечным, то каждая траектория луча имеет точку поворота на конечном расстоянии от оси, определяемом соотношением (3.2)
. Но так как этот профиль является одним из простейших для понимания процессов распространения, мы будем его использовать как составной элемент при анализе волноводов параболического профиля с однородной оболочкой. Так как профиль является бесконечным, то каждая траектория луча имеет точку поворота на конечном расстоянии от оси, определяемом соотношением (3.2)
| (7.2) |
где последнее выражение справедливо в параксиальном приближении. Таким образом, чем больше угол θz(0) или чем меньше β, тем дальше от оси расположена точка поворота. Поскольку не существует лучевых траекторий, являющихся решениями уравнения (4.3), расположенных за точками поворота, то все лучи являются направляемыми, а инвариант β направляемых лучей удовлетворяет условию
| (7.3) |
Подставляя (7.2) в уравнение (4.3) и используя замену переменных ![]() , получаем интеграл по аргументу ω, который легко вычисляется. Итак, траектория луча определяется соотношениями
, получаем интеграл по аргументу ω, который легко вычисляется. Итак, траектория луча определяется соотношениями
| (7.4) |
где zp - полупериод траектории луча, вычисленный аналогичным образом с помощью (4.6). Используя ту же замену переменных, из (4.5) можно вычислить оптическую длину пути
| (7.5) |
тогда как геометрическая длина пути LP выражается через полный эллиптический интеграл 2-го рода E(v) (согласно соотношению 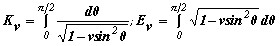 ). Однако в приближении слабонаправляющего волновода (6.5) при ∆<<1 можно получить упрощенное выражение
). Однако в приближении слабонаправляющего волновода (6.5) при ∆<<1 можно получить упрощенное выражение
| (7.6) |
Наконец, время прохождения луча (5.2) определяется непосредственно из соотношений (7.4), (7.5) как
| (7.7) |
Практическое моделирование.
Моей практической задачей являлось построение лучевой траектории в планарном волноводе градиентного параболического профиля. Для этого мне потребовалось написать программу, которая бы позволила пользователю, задавая параметры (коэффициенты преломления, радиус сердцевины волновода и начальный угол входа луча) посмотреть, как проходит луч по волноводу.
Для этого мной был использован математический пакет “Mathcad 7.0 PRO”. Данный пакет позволяет решать уравнения различного типа, так же может строить графики различных функций.
Во-первых, вводятся начальные параметры:
n0 - максимальный преломления,
n1 - коэффициент преломления оболочки,
θ1 - начальный угол входа луча в центральной части сердцевины (точка максимального коэффициента преломления),
ρ - радиус сердцевины.
Во-вторых, производиться расчёт критического угла входа (угол входа должен быть меньше критического угла!) θ0 и лучевой инвариант β.
В-третьих, рассчитывается удаление каустики поворота от оси сердцевины - x0.
В-четвёртых, рассчитывается длина полупериода Z0 и время его прохождения t.
Конечным результатом работы является исчисленное время прохождения полупериода и график, на котором изображена траектория луча в сердцевине (только в сердцевине!) волновода.
Листинг программы и результаты её работы прилогаются.
Заключение
В данной работе были рассмотрены законы, по которым происходит направление луча света в светопроводящей среде (волноводе). На примере планарного волновода параболического профиля были рассмотрены принципы и произведены расчёты. По полученным результатам можно оценить значения лучевых параметров и рассчитать приблизительное время прохождения луча по волноводу определённой длины. Использую данную информацию, законы и формулы мы можем также построить и рассмотреть приблизительные траектории лучей проходящих в волноводе при различных значениях коэффициентов преломления и начальных углах входа луча в волновод.
Список используемых источников
- Алан Снайдер, Джон Лав. Теория оптических волноводов: Пер. с англ. - Москва: Радио и связь, 1987г. - 656 с.: ил.
- Кацеленбаум Б. З. Теория нерегулярных волноводов.-Москва: Изд. АН СССР, 1961г. - 216 с.
- Маркузе Д. Оптические волноводы: Пер. с англ.-Москва: Мир. 1974г. - 576 с.
- Унгер Х.-Г. Планарные и волоконные волноводы: Пер. с англ. - Москва: Мир, 1980г. - 656 с.
Приложение 1.
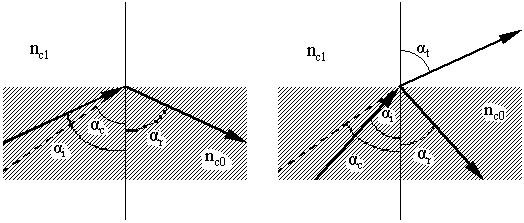
Отражение и преломление плоских волн и лучей, падающих на плоскую границу раздела между двумя полубесконечными однородными средами, определяется законами Снелля. Обозначим углы падения, отражения и преломления через соответственно αi, αr, αt, а показатели преломления сред nc0(от куда идёт луч) и nc1(на раздел с которой он падает), а также критический угол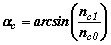 .
.
Если αi> αс, то падающий луч испытывает полное внутреннее отражение, а при этом αr=αi, но если αi> αс, то имеется как частичное отражение, так и частичное преломление (или прохождение), а углы удовлетворяют соотношению
|
Для планарных волноводов удобно выразить закон Снелля через углы скольжения, то есть θz=π/2-αi=π/2-αr, θt=π/2-αt, θc=π/2-αc.
Приложение 2.
Профиль, n2(x) |
|
Полупериод лучевой траектории, |
|
Длина пути, LP |
|
Оптическая длина пути, L0 |
|
Время прохождения луча, t |
|
Листинг программы
Пример работы программы
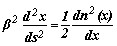 .
.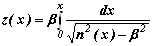 ,
,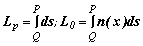 ,
,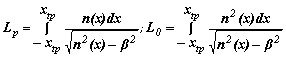 .
.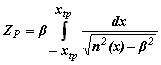 .
.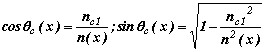 .
.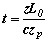 .
.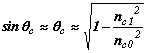
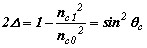
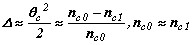 или
или 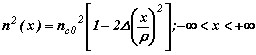 ,
,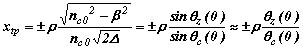 ,
,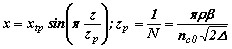 ,
,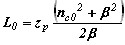 ,
,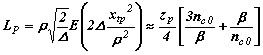
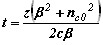 .
.