Гамма функции

1. Бэта-функции 6

Бэта – функции определяются интегралом Эйлера первого рода:

= (1.1)

сходятся при .Полагая =1 – t получим:

= - =

т.e. аргумент и входят в симетрично. Принимая во внимание тождество

по формуле интегрирования почестям имеем

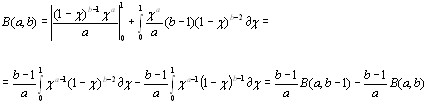
Откуда

= (1.2)

7

При целом b = n последовательно применяя(1.2)

Получим

(1.3)

при целых = m,= n,имеем

но B(1,1) = 1,следовательно:

Положим в (1.1) .Так как график функции симметрична относительно прямой ,то

8

и в результате подстановки ,получаем

полагая в(1.1) ,откуда ,получим

(1.4)

разделяя интеграл на два в пределах от 0 до 1 и от 1 до и применение ко второму интегралу подстановки ,получим

=

2. Гамма-функция 9

Гамма функцию определяет интеграл Эйлера второго рода

Γ(a) = (2.1)

сходящийся при 0.Положим =ty,t > 0 ,имеем

Γ(a) =

и после замены , через и t через 1+t ,получим

Умножая это равенство и интегрируя по t и пределах от 0 до, имеем:

или на основании (1.4) и после изменения в правой части порядка интегрирования ,получаем:

10

откуда

(2.2)

заменяя в (2,1) ,на и интегрируем по частям

получаем рекурентною формулу

(2.3)

так как

но при целом имеем

(2.4)

то есть при целых значениях аргумента гамма-функция превращается в факториал.Порядок которого на единицу меньше взятого значения аргумента.При n=1 в (2.4) имеем

Интеграл

сходится при каждом ,поскольку ,и интеграл при сходится.

В области , где - произвольное положительное число, этот интеграл сходится равномерно, так как и можна применить признак Веерштраса. Сходящимся при всех значениях является и весь интеграл так как и второе слогаемое правой части является интегралом, заведомо сходящимся при любом.Легко видеть что интеграл сходится пов любой области где произвольно.Действительно для всех указаных значений и для всех ,и так как сходится, то выполнены условия признака Веерштрасса. Таким образом , в области интеграл cходится равномерно.

Отсюда вытекает непрерывность гамма функции при.Докажем дифференцируемость этой функции при .Заметим что функция непрерывна при и, и покажем ,что интеграл :

12

сходится равномерно на каждом сегменте , . Выберем число так , чтобы ; тогда при .Поэтому существует число такое , что и на.Но тогда на справедливо неравенство

и так как интеграл сходится, то интеграл сходится равномерно относительно на . Аналогично для существует такое число , что для всех выполняется неравенство . При таких и всех получим , откуда в силу признака сравнения следует , что интеграл сходится равномерно относительно на . Наконец , интеграл

в котором подынтегральная функция непрерывна в области

, очевидно, сходится равномерно относительно на . Таким образом , на интеграл

13

сходится равномерно , а, следовательно , гаммма функция бесконечно дифференцируема при любом и справедливо равенство

.

Относительно интеграла можна повторить теже рассуждения и заключить, что

По индукции доказывается , что Г-функция бесконечно дифференцируема прии для ее я -ой производной справедливо равенство

Изучим теперь поведение - функции и построим єскиз ее графика .

Из выражения для второй производной -функции видно, что для всех . Следовательно, возрастает. Поскольку , то по теореме Роля на сегменте (1,2)производная при и при , т. е. Монотонно убывает на и монотонно возрастает на . Далее , поскольку , то при . При из формулы следует , что при .

14

Равенство , справедливое при , можно использовать при распространении - функции на отрицательное значение .

Положим для, что . Правая часть этого равенства определена для из (-1,0). Получаем, что так продолженная функция принимает на (-1,0) отрицательные значения и при , а также при функция .

Определив таким образом на , мы можем по той же формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением окажется функция, принимающая положительные значения и такая, что при и . Продолжая этот процесс, определим функцию , имеющею разрывы в целочисленных точках (см. рис.1)

Отметим еще раз, что интеграл

определяет Г-функцию только при положительных значениях , продолжение на отрицательные значения осуществлено нами формально с помощью формулы приведения .

15

(рис.1)

4. Вычисление некоторых интегралов. 16

Формула Стирлинга

где m > -1,n > -1.Полагая , что ,имеем

и на основании (2.2) имеем

(3.1)

В интеграле

Где k > -1,n > 0,достаточно положить

17

Интеграл

Где s > 0,разложить в ряд

=

где дзетта функция Римана

Рассмотрим неполные гамма функции (функции Прима)

связанные неравенством

Разлагая, в ряд имеем

18

Переходя к выводу формулы Стирлинга , дающей в частности приближенное значение n! при больших значениях n ,рассмотрим предварительно вспомогательную функцию

(3.2)

Непрерывна на интервале (-1,) монотонно возрастает от до при изменении от до и обращаются в 0 при u = 0.Так как

то при u > 0 и при u < 0 , далее имеем

И так производная непрерывна и положительна во всем интервале ,удовлетворяет условию

19

Из предыдущего следует, что существует обратная функция, определенная на интервале непрерывная и монотонно возрастающая в этом интервале,

Обращающаяся в 0 при v=0 и удовлетворяющая условие

(3.3)

Формулу Стирлинга выведем из равенства

полагая ,имеем

Положим далее введенная выше обратная функция, удовлетворяющая условиям u = -1при ,и при .Замечая что(см.3.2)

20

имеем

,

полагая на конец ,,получим

или

в пределе при т.е. при (см3.3)

откуда вытекает формула Стирлинга

которую можно взять в виде

21

(3.4)

где ,при

для достаточно больших полагают

(3.5)

вычисление же производится при помощи логарифмов

если целое положительное число, то и (3.5) превращается в приближенную формулу вычисления факториалов при больших значениях n

приведем без вывода более точную формулу

где в скобках стоит не сходящийся ряд.

5. Примеры вычисления интегралов 22

Для вычисления необходимы формулы:

Г()

Вычислить интегралы

23

Запорізький державний університет

Зав. каф. Математичного аналізу

д. т. н. проф. ____ С.Ф. Шишканова

_________________________ 2002р.

ГАМА ФУНКЦІЇ

Ст..гр.. 8221-2

Керівник

Ст. викладач

Запоріжжя 2002.

Реферат ...................................4

введение ...................................5

1. Бета функции……………………………………………..............6
2. Гамма функции. ...................................9
3. Производная гамма функции ..................................11
4. Вычисление интегралов формула Стирлинга............................16
5. Примеры вычеслений ..................................22

вывод ..................................24

Список литературы……………………………………………..............25

Реферат

Обьект иследований: гамма и ее приложения.

В работе идет речь о представлении бета и гамма функций с помощью интегралов Эйлера соответствено первого и второго рода. И о их применении для вычисления интегралов.

Ключевые слова:

ГАММА И БЕТА ФУНКЦИЯ, ИНТЕГРАЛ ЭЙЛЕРА, ПРОИЗВОДНАЯ, ПРЕДЕЛ.

Выделяют особый класс функций, представимых в виде собственого либо несобственого интеграла, который зависит не только от формальной переменной, а и от параметра.

Такие функции называются интегралами зависящими от параметра. К их числу относятся гамма и бета функции Эйлера.

Бета функции представимы интегралом Эйлера первого рода:

гамма функция представляется интегралом Эйлера второго рода:

Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях.

Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.

2. Математический анализ часть 2:

Ильин О.А., Садовничий В.А., Сендов Бл.Х.,М.,”Московский университет”,1987

3. Сборник задач по математическому анализу:

Демидович Б.П.,М.,Наука,1966

4. Интегралы и ряды специальные функции:

Прудников А.П., Брычков Ю.А.,М.,Наука,1983

5. Специальные функции:

Кузнецов , М.,”Высшая школа”,1965