Решение тригонометрических неравенств

по теме:

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ

НЕРАВЕНСТВ

работу выполнил:

студент Ставропольского

Государственного Университета

IV курса, Физ-Мат Факультета,

отделения МИИТ, гр. ”Б”

Неботов Виталий Дмитриевич

Ставрополь 1997 г.

СОДЕРЖАНИЕ :

Стр.

1. Вступительное слово....................................................................................3

2. Этапы “большого пути”...............................................................................3

3. Тригонометрические отношения.................................................................3

4. Тригонометрические функции.....................................................................3

5. Тригонометрические уравнения...................................................................3

6. Тригонометрические неравенства................................................................3

7. Способы решения тригонометрических неравенств...................................4

8. В помощь начинающему ..............................................................................5

9. Заключение....................................................................................................5

10. Список использованной литературы..........................................................6

Решение тригонометрических неравенств стоит в одном ряду с такими важными темами, как решение числовых неравенств и решение систем неравенств с одной переменной. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Еще греки, на заре человечества, считали тригонометрию важнейшей из наук, ибо геометрия - царица математики, а тригонометрия - царица геометрии. Поэтому и мы, не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом.

С чего же начинается обучение решению тригонометрических неравенств в школе? Естественно, с самих тригонометрических функций. Сначала даются сами отношения sin x, cos x, tg x и ctg x. Делается это на конкретных примерах рассматриваемых треугольников. Затем делается важный переход от синуса и косинуса в прямоугольном треугольнике к этим же отношениям, но уже в произвольном угле. Sin и cos освобождаются от конкретной геометрической привязки и эти понятия становятся шире.

Следующим этапом введения понятий sin x, cos x, tg x и ctg x является рассмотрение функциональных зависимостей или попросту функций y = sin x, y = cos x, y = tg x и y = ctg x соответственно. На этом этапе даются все основные свойства этих функций, рассматриваются области определения и значений, промежутки знакопостоянства, и главное - графики этих функций. Анализ функции нельзя считать полным, так как еще не усвоен и не применялся аппарат дифференцирования, но для решений тригонометрических неравенств почва уже подготовлена и ребята хорошо “вооружены” теоретическими знаниями.

Наконец последний подготовительный этап “большого пути” - решение тригонометрических уравнений. Здесь отрабатываются последние нюансы, ребенок учится оперировать сложными тригонометрическими конструкциями, но главное, именно сейчас даются основные тригонометрические тождества и производные от них. Помощь этого тригонометрического аппарата трудно переоценить. Знаниями полученными здесь и сейчас ученики смогут пользоваться всю оставшуюся жизнь. Мощь блока тригонометрических тождеств поистине потрясает, так как с его помощью управляться с громоздкими, “трехэтажными” тригонометрическими выражениями становится также просто, как и с алюминиевой вилкой.

И только теперь, хорошо освоив все предыдущие разделы ученики подходят к нашей теме, а именно решение тригонометрических неравенств. Естественно начинают решение таких неравенств с самых простейших: sin x > a, sin x < a; cos x > a, cos x < a; tg x > a, tg x < a. Затем, освоив данные неравенства, постепенно переходят к более сложным неравенствам, содержащим несколько функций одновременно, содержащим разные функции в разных степенях и ко всевозможным их комбинациям. Естественно, для мальчиков и девочек 13-14 лет этот материал простым и легким не назовешь, он требует аналитического склада ума, умения мыслить абстрактно, а главное быстро. Поэтому изучение этого материала без какого-либо дополнительного инструментария было бы весьма и весьма затруднительным. Но, к счастью, это не так: был найден простой и удобный, а главное наглядный инструментарий позволяющий легко решать такие простейшие тригонометрические неравенства. На самом деле их даже два.

У внимательного читателя может возникнуть резонный вопрос, ради чего было огород городить, если с помощью вашего “удивительного” инструментария можно решать только простейшие неравенства, которые и так, как-нибудь можно решить. На это можно ответить, что любое тригонометрическое неравенство, каким бы большим и запутанным оно не казалось вначале, можно с помощью тождественных преобразований свести к простейшему (нескольким простейшим) тригонометрическим неравенствам. Затем мы можем решить их либо используя тригонометрический круг, либо сам график полученной функции.

В действительности в школьном курсе нет жесткой регламентации каким из указанных двух способов пользоваться при решении тригонометрических неравенств. Здесь выбор полностью за данным конкретным преподавателем. Учителя вольны использовать как один, так и другой способы, но мне кажется, что тригонометрический круг все же нагляднее и поняв один раз его принцип начинаешь пользоваться им также свободно как и дышать, к тому же он просто компактнее и занимает в тетради меньше места. По-видимому идеальным вариантом является совместное, взаимодополняющее использование обоих выше перечисленных методов решения простейших тригонометрических неравенств.

Итак, тригонометрический круг единичного радиуса (вы можете видеть его изображение рядом). Почему его радиус взят за единицу, а не скажем за двойку или пятерку. Ответ очевиден: угол здесь изображается радиусом и отрезком оси ОХ, и если мы опустим перпендикуляр из точки пересечения радиуса с окружностью на ось ОХ, по получим прямоугольный треугольник. В тригонометрическом круге длина отрезка ОУ принята за sin x, a длина отрезка ОХ за cos x. По теореме Пифагора ОХ2 + ОУ2 = R2. Таким образом, подставив синус и косинус получим: sin2x + cos2x = 1. Вот так мы и вышли на основное тригонометрическое тождество. Именно поэтому тригонометрический круг единичного радиуса.

Как я уже сказал, мы, с помощью тригонометрических тождеств, приводим неравенство к простейшему виду, а затем решаем его используя тригонометрический круг или график. Для успешного решения необходимо также знать следующее:

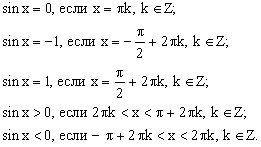
О косинусе можно сказать следующее:

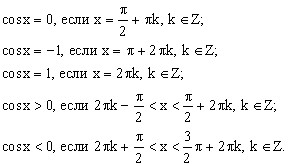
И наконец тангенс, вобравший в себя все самое лучшее из синуса и косинуса:

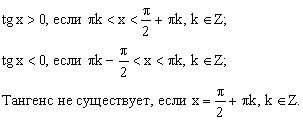
Вооруженный такими знаниями, не только школьник, но и простой человек, никогда не учившийся в школе сможет быстро освоить и без труда решать эти “загадочные” тригонометрические неравенства.

Список использованной литературы:

1. В. С. Крамор, Повторяем и систематизируем школьный курс

алгебры и начал анализа, Москва, Просвещение, 1990 г.

2. С. А. Теляковский, Алгебра, учебник для 8 класса средней школы,

Москва, Просвещение, 1987 г.

3. Личные заметки и наблюдения автора.