Развитие продуктивного мышления на уроках математики

Рецензия

на дипломную работу студента 5 курса физико-математического факультета АГПИ Гудырина Сергея Николаевича.

В дипломной работе, озаглавленной “Развитие продуктивного мышления на уроках математики” автор дал определение оптимальных условий развития продуктивного мышления на уроках математики в средней школе, а также указал конкретные методы для эффективного развития продуктивного мышления школьников.

Для реализации этой цели Гудыриным С. Н. была разработана система приемов решения нестандартных задач по математике с учащимися 7-го класса. Используя эти приемы автор сумел заметно активизировать творческую мыслительную деятельность учащихся, что представлено в гл. 3 “Условия и задачи развития продуктивного мышления в учебной деятельности”.

Несомненным достоинством работы является применение оригинальной методики для выявления уровня экономичности мышления.

Результаты эксперимента, проведенного в СШ № 18 показали на сравнительном анализе результатов двух классов, что навыки продуктивного мышления у школьников формируются значительно быстрее с использованием специально подобранных методических приемов решения нестандартных задач.

Предлагаемая на рецензию дипломная работа представляет интерес не просто как частная методическая разработка, а как и общий методический подход к развитию продуктивного мышления на уроках математики современной средней школы.

Работа выполнена полностью самостоятельно и несомненно заслуживает оценки “отлично”.

Старший преподаватель

кафедры ОИВТ Генералов Г. М.

Подпись Генералова Г. М. заверяю.

Начальник отдела кадров Сапельникова А. Г.

Рецензия

на дипломную работу “Развитие продуктивного мышления на уроках математики“ студента 5 курса физико-математического факультета АГПИ Гудырина Сергея Николаевича.

В работе Гудырина С. Н. исследуется проблема организации учебной деятельности на уроках математики, направленной на развитие навыков продуктивного мышления школьников.

В теоретической части работы излагаются вопросы, касающиеся проблем теории продуктивного мышления, что позволило определить понятие “продуктивное мышление” и выделить критерии его развития. Материал изложен интересно и достаточно подробно, с использованием большого количества литературы.

Для доказательства сформулированной автором гипотезы был использован комплексный метод, который включает в себя оригинальные методики определения уровня сформированности продуктивного мышления и его развития.

Исходя из экспериментальных данных были построены конкретные рекомендации к курсу математики.

Актуальным моментом дипломной работы является её практическая направленность, поиск применения теории на практике.

Данная работа заслуживает высокой оценки “отлично”.

Доктор психологических

наук, доцент, заведующий

кафедрой педагогики и

психологии начального

обучения Тимофеев Ю. П.

Подпись Тимофеева Ю. П. заверяю.

Начальник отдела кадров Сапельникова А. Г.

Министерство образования Российской Федерации

Астраханский государственный педагогический институт им. С. М. Кирова

Кафедра математическогоанализа

Развитие продуктивного мышления на уроках математики

ДИПЛОМНАЯ РАБОТА

студента ФМФ Гудырина Сергея Николаевича

Научные руководители: кандидат психологическихнаук, доцент, заведующий кафедрой психологииКайгородов Борис Владиславович старший преподаватель кафедрыматематического анализаСикорская Людмила Витальевна

Известно, что в разное время вопросами мышления занимались ученые-психологи различных школ и направлений.

Как процесс репродуктивный, процесс, в результате которого не возникает ничего принципиально нового, а происходит лишь перекомбинация исходных элементов, рассматривали мышление ассоцианисты (А. Бен, Д. Гартли). В настоящее время этот подход нашел свое выражение в бихевиоризме (А. Вейс, Б. Скиннер).

Выразителями другого подхода к мышлению как к чисто продуктивному процессу являлись представители гештальтпсихологии (М. Вертгаймер, В. Келлер, К. Кофка и др.).

В трудах советских психологов продуктивность выступает как наиболее характерная, специфическая черта мышления, отличающая его от других психических процессов, и в то же время рассматривается противоречивая связь её с репродукцией.

Идеи о творческом характере мышления разрабатывались в трудах Б. Г. Ананьева, П. Я. Гальперина, А. В. Запорожеца, А. Н. Леонтьева, Н. А. Менчинской и многих других.

Среди работ, посвященных вопросам развития продуктивного (творческого) мышления при обучении математике следует отметить работы В. А. Крутецкого, Д. Пойа, Л. М. Фридмана, Е. Н. Турецкого.

Однако, при кажущемся обилии научного материала по этой тематике приходится признать, что конкретного фактического материала, позволяющего строить обучение школьников с учетом особенностей продуктивного мышления, нет. Существует множество методических пособий по курсу математики в средней школе, но в ходе нашей работы нам не встретилось ни одного, в котором были бы собраны и обобщены данные, позволяющие развивать творческое мышление школьников на уроках математики не выходя за рамки курса. И затрагивая вопрос о целесообразности нашей работы можно сказать, что данное исследование не только возможно было провести, но, на наш взгляд, и необходимо.

Целью нашего исследования являлось определение оптимальных условий и конкретных методов развития продуктивного мышления на уроках математики в средней школе.

Объектом нашего исследования выступал сам учебно-воспитательный процесс.

Предметом нашего исследования стали проблемы теории продуктивного (творческого) мышления, а также изучение способов развития продуктивного мышления на уроках математики в 7 классе.

После анализа литературы по интересующему нас вопросу мы выдвинули гипотезу, что развить творческое мышление на уроках математики, заинтересовать их математикой, привести к «открытию» математических фактов возможно только при условии использования на уроках задач нестандартных, задач, требующих известной независимости мышления, здравого смысла, оригинальности и изобретательности.

Назовем конкретные задачи, которые определили содержание и структуру нашего исследования в его теоретической и экспериментальной частях:

1. Исследовать вопрос теории мышления: существо проблемы и её историко-теоретический аспект.
2. Проанализировать вопрос, что есть понятие — продуктивное мышление.
3. Изучить основные особенности продуктивного мышления.
4. Рассмотреть некоторые психолого-педагогические принципы развития продуктивного мышления.
5. Выявить уровень сформированности продуктивного мышления в условиях современной школы (7 класс).
6. Определить способы и конкретные приемы активизации творческой мыслительной деятельности на уроках математики у учащихся 7-х классов.

В процессе нашего исследования мы использовали оригинальную методику, созданную на основе работ Калмыковой З. И. для определения уровня сформированности продуктивного мышления, а также провели серию занятий по экспериментальной методике использования нестандартных задач для активизации творческой мыслительной деятельности учащихся.

Предмет нашего исследования — творческое (продуктивное) мышления. Хотя это понятие давно употребляется в психологической литературе, его содержание дискуссионно. Обращаясь к анализу литературы, мы ставили перед собой задачу выяснить, как крупнейшие представители психологических теорий определяют понятие «творческое мышление», как решают вопрос о соотношении продуктивных и репродуктивных компонентов мыслительной деятельности.

Для зарубежной психологии весьма типичен односторонний подход к характеристике мышления: оно выступает как процесс только репродуктивный, либо продуктивный. Представителями первого подхода были ассоцианисты (А. Бэн, Д. Гартли, И. Гербарт, Т. Рибо и др.). Характеризуя мышление с идеалистических позиций они сводили суть его к отвлечению от несходных элементов, к объединению сходных элементов в комплексы, к их перекомбинации, в результате которой не возникает ничего принципиально нового.

В настоящее время репродуктивный подход нашел свое выражение в теории бихевиоризма (А. Вейс, Э. Газри, Ж. Леб, Б. Скиннер, Э. Торндайк и др.). Эта теория привлекла внимание ученых своей установкой на разработку точных методов изучения психики, на объективность подхода к анализу психических явлений, однако сам анализ бихевиористы осуществляли с позиций механистического материализма.

Хотя бихевиоризм был подвергнут резкой критике за отрицание роли внутренних, психических факторов, его идеи находят своих сторонников.

Очень явно это выражено в работах Б. Скиннера. В теоретическом плане он прямо отрицает наличие у человека такого феномена, как мышление, сводит его к обусловленному поведению, связанному с закреплением приводящих к успеху реакций, к выработке системы интеллектуальных навыков, которые могут быть сформированы принципиально тем же путем, что и навыки у животных. На этих основах им разработана «линейная» система программированного обучения, предусматривающая изложение материала, столь развернутое и детализированное, что даже самый слабый ученик при работе с ним почти не допускает ошибок, и, следовательно, у него не возникают ложные связи между стимулами и реакциями, вырабатываются правильные навыки на основе положительного подкрепления.

Выразителями второго подхода к мышлению как к чисто продуктивному процессу являются представители гештальтпсихо­логии (М. Вертгаймер, В. Келер, К. Коффка и др.). Продуктивность рассматривается ими в качестве специфической черты мышления, отличающей его от других психических процессов. Мышление возникает в проблемной ситуации, включающей в себя неизвестные звенья. Преобразование этой ситуации приводит к такому решению, в результате которого получается нечто новое, не содержащееся в фонде имеющихся знаний и не выводимое из него непосредственно на основе законов формальной логики. Существенную роль в решении проблемы играет инсайт как прямое непосредственное видение пути к нахождению искомого, способа преобразования ситуации, дающего ответ на поставленный в задаче вопрос. Гештальтисты в исследованиях мышления широко использовали задачи, при решении которых у испытуемых возникал конфликт между имеющимися знаниями и требованиями задачи, и они вынуждены были преодолевать «барьер прошлого опыта», вследствие чего сам процесс поисков неизвестного выступал особенно явно. Благодаря этому ученые получили весьма ценный материал об особенностях мыслительной деятельности (К. Дункер, Л. Секей).

Однако, придавая большое значение инсайту, «ага-переживанию», гештальтисты не показали сам механизм его возникновения, не раскрыли того, что инсайт подготовлен активной деятельностью самого субъекта, его прошлым опытом.

Выделив в качестве специфики мышления его продуктивный характер, гештальтисты резко противопоставили его репродуктивным процессам. В их экспериментах прошлый опыт, знания выступили тормозом продуктивного по своей природе мышления, хотя под влиянием накопленных фактов им все же пришлось ограничить категоричность своих выводов, признать, что знания могут играть и положительную роль в мыслительной деятельности.

Такое признание, в частности, имеется у Л. Секея, который специально останавливается на вопросе о соотношении мышления и знаний. Характеризуя репродуктивное мышление, автор отмечает, что оно предполагает воспроизведение процессов, имевших место в прошлом, допускает в них некоторые незначительные видоизменения. Он не отрицает роли прошлого опыта и в творческом мышлении, рассматривая знания как отправную точку для понимания и материал для решения проблемы.

В аспекте стоящей перед нами проблемы нас интересовал вопрос о том, каковы те признаки, на основе которых исследователи раскрывали специфику мышления, отражали ли они и в какой мере его репродуктивную и продуктивную стороны. Анализ зарубежной литературы показал, что в любом случае, когда речь шла о мышлении, говорилось о возникновении нового, но характер этого нового, источники его в различных теориях указывались неидентичные.

В репродуктивных теориях мышления новое выступало как результат усложнения или перекомбинации на основе, главным образом, сходства имеющихся элементов прошлого опыта, актуализации непосредственной связи между требованиями задачи и субъективно тождественными элементами имеющихся знаний. Само решение задачи протекает на основе либо механических проб и ошибок с последующим закреплением случайно найденного верного решения, либо актуализации определенной системы раннее сформированных операций.

В продуктивных теориях мышления новое, возникающее в результате мыслительной деятельности, характеризуется своей оригинальностью (у гештальтистов — это новая структура, новый гештальт). Оно возникает в проблемной ситуации, обычно предполагающей преодоление «барьера прошлого опыта», мешающего поиску нового, требующего понимания этой ситуации. Решение осуществляется как преобразование первоначальных проблем, но сам принцип решения возникает вдруг, внезапно, в порядке инсайта, прямого усмотрения пути решения, зависящего главным образом от объективных условий задачи и очень мало от активности самого решающего субъекта, от его собственного опыта.

Идеи о творческом характере мышления человека, о его специфике, взаимоотношениями с другими процессами, и прежде всего с памятью, о закономерностях его развития разрабатывались в исследованиях многих советских психологов (Б. Г. Ананьев, П. Я. Гальперин, А. В. Запорожец, Г. С. Костюк, А. Н. Леонтьев, А. А. Люблинская, Н. А. Менчинская, Ю. А. Самарин, Б. М. Теплов, М. Н. Шардаков, П. Я. Шеварев, Л. И. Узнадзе, Н. П. Элиава и др.). Широкое обобщение положений о сущности и специфике мышления было осуществлено С. Л. Рубинштейном.

В трудах советских психологов продуктивность выступает как наиболее характерная, специфическая черта мышления, отличающая его от других психических процессов, и в то же время рассматривается противоречивая связь ее с репродукцией.

Мышление представляет собой активную целенаправленную деятельность, в процессе которой осуществляется переработка имеющейся и вновь поступающей информации, отчленение внешних, случайных, второстепенных ее элементов от основных, внутренних, отражающих сущность исследуемых ситуаций, раскрываются закономерные связи между ними. Мышление не может быть продуктивным без опоры на прошлый опыт, и в то же время оно предполагает выход за его пределы, открытие новых знаний, благодаря чему расширяется фонд их и тем самым увеличивается возможность решения все новых и новых, более сложных задач.

В мышлении как процессе обобщенного и опосредованного познания действительности в диалектически противоречивом единстве сплетены его продуктивные и репродуктивные компоненты, причем удельный вес их в конкретной мыслительной деятельности может быть различным. Под влиянием всевозрастающих требований жизни к творческому её компоненту возникла необходимость выделить особые виды мышления — продуктивное и репродуктивное.

Следует отметить, что в советской литературе встречается возражение против выделения таких видов, поскольку любой процесс мышления продуктивен (А. В. Брушлинский). Однако, большинство психологов, изучающих мышление, считают целесообразным выделение этих видов (П. П. Блонский, Д. Н. Завалишина, Н. А. Менчинская, Я. А. Пономарев, В. Н. Пушкин, О. К. Тихомиров).

В литературе данные виды (стороны, компоненты) мыслительной деятельности называют по-разному. Как синонимы к понятию «продуктивное мышление» употребляют термины: творческое мышление, самостоятельное, эвристическое, креативное. Синонимами к репродуктивному мышлению служат термины: словесно-логическое, дискурсивное, рассудочное, рецептивное и др. Мы применяем термины продуктивное и репродуктивное мышление.

Продуктивное мышление характеризуется высокой степенью новизны получаемого на его основе продукта, его оригинальностью. Это мышление появляется тогда, когда человек, попытавшись решить задачу на основе ее формально-логического анализа с прямым использованием ему известных способов, убеждается в бесплодности таких попыток и у него возникает потребность в новых знаниях, которые позволяют решить проблему: эта потребность и обеспечивает высокую активность решающего проблему субъекта. Осознание самой потребности говорит о создании у человека проблемной ситуации (А. М. Матюшкин).

Нахождение искомого предполагает открытие не известных субъекту признаков, существенных для решения проблемы отношений, закономерных связей между признаками, тех способов, с помощью которых они могут быть найдены. Человек вынужден действовать в условиях неопределенности, намечать и проверять ряд возможных решений, осуществлять выбор между ними, подчас не имея к тому достаточных оснований. Он ищет ключ к решению на основе выдвижения гипотез и их проверки, т. е. способы опираются на известное предвидение того, что может быть получено в результате преобразований. Существенную роль в этом играют обобщения, позволяющие сокращать количество той информации, на основе анализа которой человек приходит к открытию новых знаний, уменьшать число проводимых при этом операций, «шагов» к достижению цели.

Как подчеркивает Л. Л. Гурова, весьма плодотворным в поиске пути решения проблемы оказывается ее содержательный, семантический анализ, направленный на раскрытие натуральных отношений объектов, о которых говорится в задаче. В нем существенную роль играют образные компоненты мышления, которые позволяют непосредственно оперировать этими натуральными отношениями объектов. Они представляют собой особую, образную логику, дающую возможность устанавливать связи не с двумя, как при словесном рассуждении, а со многими звеньями анализируемой ситуации, действовать, по словам Л. Л. Гуровой, в многомерном пространстве.

В исследованиях проведенных под руководством С. Л. Рубинш­тейна (Л. И. Анцыферовой, Л. В. Бруш­инским, А. М. Матюшкиным, К. А. Славской и др.), в качестве эффективного приема, используемого в продуктивном мышлении, выдвигается «анализ через синтез». На основе такого анализа искомое свойство объекта выявляется при включении объекта в ту систему связей и отношений, в которой он более явно обнаруживает данное свойство. Найденное свойство открывает новый круг связей и отношений объекта, с которыми это свойство может быть соотнесено. Такова диалектика творческого познания действительности.

В этом процессе, как отмечают многие исследователи, нередко имеет место внешне внезапное усмотрение пути решения — инсайт, «ага-переживание», причем оно часто возникает тогда, когда человек непосредственно не был занят решением проблемы. Реально такое решение подготовлено прошлым опытом, зависит от предшествующей аналитико-синтетической деятельности и прежде всего — от достигнутого решающим уровня словесно-логического понятийного обобщения (К. А. Славская). Однако, сам процесс поисков решения в значительной своей части осуществляется интуитивно, под порогом сознания, не находя своего адекватного отражения в слове, и именно потому его результат, «прорвавшийся» в сферу сознания, осознается как инсайт, якобы не связанный с ранее осуществлявшейся субъектом деятельностью, направленной на открытие новых знаний.

Включая в продуктивное мышление его имманентные, неосознаваемые компоненты, отдельные исследователи нашли экспериментальные приемы, позволяющие выявить некоторые особенности этих компонентов.

Интересный методический прием для экспериментального изучения интуитивных компонентов продуктивного мышления применил В. Н. Пушкин. Он предлагал испытуемым такие наглядные задачи (моделирующие шахматные игры, «игру в 5» и др.), решение которых могло быть прослежено глазами. Эти движения глаз регистрировались с помощью электроокулографической методики. Путь движения глаз соотносился с особенностями решения задачи и со словесными отчетами о нем. Исследование показало, что человек, решая проблему, собирает на основе анализа наглядной ситуации гораздо больше информации, чем осознает сам.

Большое влияние на решение проблемы, как показали результаты исследований грузинских психологов, принадлежащих к школе Д. Н. Узнадзе, может оказать наличие установки, т. е. внутреннего неосознаваемого состояния готовности к действию, определяющей специфику всей осуществляемой мыслительной деятельности.

Применив метод введения вспомогательных задач, Я. А. Поно­марев выявил ряд закономерностей влияния вспомогательных задач на решение проблем. Наибольший эффект достигается тогда, когда человек на основе логического анализа уже убедился в том, что не может решить испробованными им способами задачу, но еще не потерял веры в возможность успеха. При этом вспомогательная задача сама по себе должна быть не столь интересной, чтобы полностью поглотить сознание решающего, и не столь легкой, чтобы ее решение могло быть выполнено автоматически. Чем меньше автоматизирован способ решения, тем легче его перенос на решение основной задачи — проблемы.

Как показали эксперименты, использовав содержащуюся во второй задаче подсказку, испытуемый обычно считал, что позднее найденное решение основной проблемы никак не связано с решением вспомогательной задачи. Ему казалось, что решение затруднявшей его проблемы пришло внезапно, в порядке инсайта. Если вспомогательную задачу давали до основной, то она не оказывала ни какого влияния на последующие действия испытуемых.

Хотя мышление как процесс обобщенного и опосредованного познания действительности всегда включает в себя элементы продуктивности, удельный вес ее в процессе мыслительной деятельности может быть различным. Там, где удельный вес продуктивности достаточно высок, говорят о собственно продуктивном мышлении как особом виде мыслительной деятельности. В результате продуктивного мышления возникает нечто оригинальное, принципиально новое для субъекта, т. е. степень новизны здесь высока. Условие возникновения такого мышления — наличие проблемной ситуации, способствующей осознанию потребности в открытии новых знаний, стимулирующей высокую активность решающего проблему субъекта.

Новизна проблемы диктует новый путь ее решения: скачкообразность, включение эвристических, «поиско­вых» проб, большую роль семантики, содержательного анализа проблемы. В этом процессе наряду с словесно-логическими, хорошо осознанными обобщениями, очень важны обобщения интуитивно-практические, не находящие сначала своего адекватного отражения в слове. Они возникают в процессе анализа наглядных ситуаций, решения конкретно-практических задач, реальных действий с предметами или их моделями, что значительно облегчает поиск неизвестного, однако сам процесс этого поиска находится вне ясного поля сознания, осуществляется интуитивно.

Вплетаясь в сознательную деятельность, будучи подчас растянутым во времени, нередко весьма длительном, процесс интуитивно-практического мышления осознается как мгновенный акт, как инсайт благодаря тому, что в сознание сначала «прорывается» результат решения, в то время как путь к нему остается вне его и осознается на основе последующей более развернутой, осознанной мыслительной деятельности.

В результате продуктивного мышления происходит становление психических новообразований — новых систем связи, новых форм психической саморегуляции, свойств личности, ее способностей, что знаменует сдвиг в умственном развитии.

Итак, продуктивное мышление характеризуется высокой новизной своего продукта, своеобразием процесса его получения и, наконец, существенным влиянием на умственное развитие. Оно является решающим звеном в умственной деятельности, так как обеспечивает реальное движение к новым знаниям.

С психологической точки зрения нет принципиальной разницы между продуктивным мышлением ученого, открывающего объективно новые, еще не ведомые человечеству закономерности окружающего мира, и продуктивным мышлением ученика, делающего открытие нового лишь для него самого, так как в основе лежат общие психические закономерности. Однако условия поиска новых знаний у них весьма различны, как различен и уровень мыслительной деятельности, приводящей к открытию.

Для того чтобы как-то обозначить эти различия большинство исследователей предпочитают в отношении такого вида мышления школьников употреблять термин «продуктивное мышление», а термином «творческое мышление» обозначать высшую ступень мыслительной деятельности, осуществляемую теми, кто открывает принципиально новые для человечества знания, создает нечто оригинальное, не имеющее себе аналога.

Характеризуясь меньшей продуктивностью, репродуктивное мышление тем не менее играет важную роль и в познавательной, и в практической деятельности человека. На основе этого вида мышления осуществляется решение задач знакомой субъекту структуры. Под влиянием восприятия и анализа условий задачи, ее данных, искомого, функциональных связей между ними актуализируются ранее сформированные системы связей, обеспечивающие правильное, логически обоснованное решение такой задачи, адекватное отражение его в слове.

Репродуктивное мышление имеет большое значение в учебной деятельности школьников. Оно обеспечивает понимание нового материала при его изложении преподавателем или в учебнике, применение знаний на практике, если при этом не требуется их существенного преобразования и т. д. Возможности репродуктивного мышления прежде всего определяются наличием у человека исходного минимума знаний, оно, как показали исследования, легче поддается развитию, чем мышление продуктивное, и в то же время играет немалую роль в решении новых для субъекта проблем. В этом случае оно выступает на начальном этапе, когда человек пытается решить новую для него задачу известными для него способами и убеждается в том, что знакомые способы не обеспечивают ему успеха. Осознание этого приводит к возникновению «проблемной ситуации», т. е. активизирует продуктивное мышление, обеспечивающее открытие новых знаний, формирование новых систем связей, которые позднее обеспечат ему решение аналогичных задач. Как уже отмечалось процесс продуктивного мышления скачкообразен, часть его осуществляется подсознательно, без адекватного отражения в слове. Сначала в слове находит выражение его результат («Ага! Нашел! Догадался!»), а затем — сам путь к нему.

Осознание найденного субъектом решения, его проверка и логическое обоснование вновь осуществляются на основе репродуктивного мышления. Таким образом, реальная деятельность, процесс самостоятельного познания окружающей действительности — результат сложного переплетения, взаимодействия репродуктивного и продуктивного видов мыслительной деятельности.

Решение задачи исследования творческого мышления предполагает выделение совокупности индивидуальных особенностей мышления, формирующихся качеств ума от которых зависит легкость овладения новыми знаниями, широта переноса, применения этих знаний на практике.

Для их обоснованного выделения следует прежде всего обратиться к анализу некоторых литературных данных об индивидуальных особенностях мыслительной деятельности школьников. Затем, опираясь на наше представление о сущности продуктивного мышления учащихся, нужно найти среди них те, которые, по нашему мнению, должны играть ведущую роль в умственной деятельности школьников при относительно самостоятельном овладении ими новыми знаниями, при решении задач-проблем, определяя характер этой деятельности.

Понятие «интеллект» очень широко используется в научной литературе, однако до сих пор нет более или менее полного однозначного определения его содержания, структуры, факторов, в него входящих, взаимоотношений между ними. Теории структуры интеллекта весьма противоречивы.

В однофакторной (точнее, бифакторной) теории интеллекта (C. Spearmаn) за основу интеллекта берется общий для выполнения умственной деятельности генеральный фактор q, выражающий по мнению Ч. Спирмена, «общую умственную энергию», умственную активность человека, которая сочетается с множеством специальных факторов, не коррелирующих друг с другом. Насколько возможно судить по применяемым для определения умственных способностей тестам, за фактором q лежит способность к обобщению.

В мультифакторной теории (E. L. Thorndike, E. Hagen; L. L. Thurston) в основу интеллекта включено множество специальных, независимых друг от друга факторов, число которых имеет тенденцию возрастать. Наличие большого числа факторов Дж. Гилфорд считает вполне закономерным, поскольку они отражают содержание столь сложного феномена как интеллект (см. сб.: Психология мышления, 1965).

В промежуточной, «иерархической» теории интеллекта (Ph. Vernon и др.) сделана попытка связать генеральный фактор q со множеством специальных факторов через промежуточные факторы — вербальный и невербальный интеллект, каждый из которых определяет различные стороны способностей.

Для решения стоящей перед нами проблемы важно учесть данные о соотношении между интеллектом и продуктивным (творческим, «креативным») мышлением. Создатели первых вариантов тестовых методик Бине-Симона (L., M. Terman и др.) считали совершенно очевидным, что «коэффициент интеллекта» — IQ непосредственно связан с творческим мышлением, входящим в интеллект. Более поздние исследования показали, что дети с высоким IQ далеко не всегда хорошо решают задачи творческого характера.

Представляют значительный интерес те показатели, по которым судят о творческом мышлении. К ним относятся оригинальность мысли, возможность получения ответов, далеко отклоняющихся от привычных; быстрота и плавность (fluency) возникновения необычных ассоциативных связей; «восприимчивость» к проблеме, ее непривычное решение; беглость мысли как количество ассоциаций, идей, возникающих в единицу времени в соответствии с некоторым требованием; способность найти новые, непривычные функции ответа или его части (K. Duncker, A. S. Luchins, E. N. Luchins, J. P. Guilford и др.). Дж. Гилфорд считает, что все интеллектуальные способности в какой-то мере творческие, но наиболее явно они проявляются в дивергентном мышлении как способности давать необычные ответы на стандартизированные тесты. П. Торренс полагал, что в творческом мышлении появляется способность к постановке проблем, чувствительность к недостаткам в имеющихся знаниях, возможность построения гипотез об отсутствующих элементах этих знаний и т. п.

Созданы целые батареи тестов, направленные на выявление указанных особенностей мыслительной деятельности. На их основе вычисляется специальный «коэффициент творческого потенциала детей» («creativity»).

Во многих работах о творческом мышлении основными его показателями считаются такие, которые отражают степень отклонения от привычного решения, преодоления «барьеров прошлого опыта». С целью их выявления используются искусственные проблемы, предполагающие резкое столкновение имеющегося опыта с требованиями задачи, они предполагают необычные решения, нарушающие то, что диктуется опытом жизни.

Мы подходим к решению проблемы взаимоотношения интеллекта и продуктивного мышления (включая и его высшую ступень — творческое мышление) следующим образом. Интеллект человека (или его ум) характеризуется мышлением, взятым в аспекте индивидуальных различий. Самый существенный признак отличающий мышление от других психических процессов,— направленность на открытие новых знаний, т. е. его продуктивность. В соответствии с этим возможности человека к более или менее самостоятельному открытию новых знаний, определяемые (при наличие других необходимых условий) уровнем развития продуктивного мышления, составляют основу, «ядро» его интеллекта.

Рассматривая индивидуально-типические компоненты продуктив­ного мышления, мы ставили перед собой задачу выделить те его особенности, от которых зависит легкость овладения однородными знаниями, темп продвижения в них, т. е. связывали его с понятием общих способностей. У школьников эти свойства их психики обуславливают успешность учебной деятельности, быстроту и легкость в овладении новыми знаниями, широту их переноса, т. е. выступают как их общие способности к учению. Для их обозначения в психологии широко используют термин «обучаемость».

Чем выше обучаемость, тем быстрей и легче приобретает человек новые знания, тем свободнее оперирует ими в относительно новых условиях, тем выше, следовательно и темп его умственного развития. Вот почему мы полагаем, что обучаемость, наряду с фондом действенных знаний, т. е. тех, которые человек применяет на практике, входит в структуру умственного развития.

Об умственных способностях человека судят не потому, что он может сделать на основе подражания, усвоить в результате подробного, развернутого объяснения. Ум человека проявляется в относительно самостоятельном приобретении, «открытии» новых для себя знаний, в широте переноса этих знаний в новые ситуации, при решении нестандартных, новых для него задач. В этой стороне психики находит свое выражение продуктивное мышление, его особенности проявляются в формирующихся у человека качествах ума, определяя уровень и специфику обучаемости личности. Эти особенности, свойства мыслительной деятельности учащихся, качества их ума и есть компоненты обучаемости, они входят в ее структуру, а своеобразие их сочетаний определяет многообразие индивидуальных различий в обучаемости учащихся.

Одно из важнейших качеств ума — его глубина. Это качество проявляется в степени существенности признаков, которые человек может абстрагировать при овладении новым материалом, при решении проблем, и в уровне их обобщенности. Противоположное качество — поверхностность ума. Оно видно по выделению внешних, лежащих как бы на поверхности наблюдаемых явлений признаков, по установлению случайных связей между ними, что отражает низкий уровень их обобщенности.

Продуктивное мышление предполагает не только широкое использование усвоенных знаний, но и преодоление барьера прошлого опыта, отхода от привычных ходов мысли, разрешение противоречий между актуализированными знаниями и требованиями проблемной ситуации, оригинальность решений, их своеобразие. Эту сторону мышления чаще всего обозначают как гибкость ума, динамичность, подвижность и т. д. Наиболее удачен первый термин (два других чаще употребляются в контексте психофизиологических работ). При гибком уме человек легко переходит от прямых связей к обратным, от одной системы действий к другой, если этого требует решаемая задача, он может отказаться от привычных действий и т. д. Инертность ума проявляется в противоположном: в склонности к шаблону, в трудности переключения от одних действий к другим, в длительной задержке на уже известных действиях, несмотря на наличие отрицательного подкрепления и т. д.

Г. П. Антонова, исследуя гибкость мышления при решении разнообразных задач, отмечает устойчивость этого качества и наличие весьма существенных различий по суммарному «показателю гибкости» мышления школьников одного и того же возраста: для крайних групп — наиболее и наименее развитых и исследованных ею школьников этот показатель равен соответственно 12,5% и 89%, т. е. один показатель превышает второй более чем в 6 раз!

Для творческого решения проблем важно не только выделить требуемые ситуацией существенные признаки, но и, удерживая в уме всю их совокупность, действовать в соответствии с ними не поддаваясь на влияние внешних, случайных признаков анализируемых ситуаций. Эту сторону мыслительной деятельности обозначали как устойчивость ума. Она проявляется в ориентации на совокупность выделенных ранее значимых признаков, несмотря на провоцирующее действие случайных признаков новых задач того же типа. Трудности в ориентации на ряд признаков, входящих в содержание нового понятия или закономерности, необоснованная смена ориентации, переход от одних действий к другим под влиянием случайных ассоциаций — показатель неустойчивости ума.

Открытие принципиально новых знаний, столь характерное для продуктивного мышления, представляет собой скачкообразный, циклический процесс, в котором в диалектически противоречивом единстве выступают как хорошо осознанные, словесно-логические компоненты, так и не находящие адекватного отражения в слове, подсознательные, интуитивно-практические компоненты. Включение интуиции в процесс поиска нового закономерно. Однако, чтобы найденные таким образом знания приобрели действенную силу, т. е. могли быть переданы другим, использованы для решения широкого круга задач, должны быть хорошо осознаны как их существенные признаки, так и способы оперирования этими знаниями. Вот почему одним из основных качеств ума, входящих в обучаемость, мы считаем осознанность своей мыслительной деятельности, возможность сделать ее предметом мысли самого решающего проблему субъекта. В близком значении употребляется термин «рефлексия».

Это качество ума проявляется в возможности выразить в слове или в других символах (в графиках, схемах, моделях) цель и продукт, результат мыслительной деятельности ( существенные признаки вновь сформированных понятий, закономерностей), а также те способы, с помощью которых этот результат был найден, выявить ошибочные ходы мысли и их причины, способы их исправления и т. п. Неосознанность мыслительной деятельности проявляется в том, что человек не может дать отчета о решении задачи (даже если оно верное), не замечает своих ошибок, не может указать те признаки, на которые он опирался, давая тот или иной ответ, и т. д.

Внешне хорошо выраженная особенность продуктивного мышления — самостоятельность при приобретении и оперировании новыми знаниями. Это качество ума проявляется в постановке целей, проблем, выдвижении гипотез и самостоятельном решении этих задач, причем существенные индивидуальные различия по этому параметру экспериментально обнаружены уже у младших школьников.

На высшем уровне развития этого качества человек не только решает сложные для себя проблемы, но и сам, без внешней стимуляции, ищет наиболее совершенные, более высокого уровня обобщенности способы их решения (этот уровень мышления Д. Б. Богоявленская назвала креативным).

В то же время на низшем уровне, при невозможности самостоятельного решения поставленной задачи, различия в продуктивности мышления проявляются в чувствительности к помощи: чем меньше помощь, которая необходима для решения, тем выше продуктивность мышления. Вот почему мы предпочитаем разграничивать самостоятельность и чувствительность к помощи.

Таковы основные, как мы полагаем, особенности продуктивного мышления, качества ума, от которых (при прочих относительно равных условиях) зависит успешность учения.

Следует лишь отметить, что выделение данных личностных свойств продуктивного мышления, качеств ума, является весьма условным. Ведь психика представляет собой чрезвычайно сложное динамическое целое, по отношению к которому невозможно, применить дихотомию: слишком тонки, плавны подчас переходы между выделяемыми при анализе ее сторонами.

В соответствии с требованиями, предъявляемыми современной школой, обучение в ней должно ориентироваться на развитие продуктивного, творческого мышления, обеспечивающего возмож­ность самостоятельно приобретать новые знания, применять их в многообразных условиях окружающей действительности.

Мы беремся утверждать, что дальнейшее совершенствование обучения не может быть осуществлено при ориентации на один, даже очень эффективный, психолого-педагогический принцип (проблем­ности, движения от абстрактного к конкретному и т. д.), неизбежно приводящий к недооценке других. Необходима реализация системы принципов, звенья которой определяются спецификой самого продуктивного мышления, особенностями его генетического развития у школьников.

Принцип проблемности отвечая специфике продуктивного мышления — его направленности на открытие новых знаний, является основным, ведущим принципом развивающего обучения.

Проблемным называется такое обучение, при котором усвоение знаний и начальный этап формирования интеллектуальных навыков происходят в процессе относительно самостоятельного решения задач-­проблем, протекающего под общим руководством учителя.

Проблемны только те задачи, решение которых предполагает хотя и управляемый учителем, но самостоятельный поиск еще неизвестных школьнику закономерностей, способов действия, правил. Такие задачи возбуждают активную мыслительную деятельность, поддерживаемую интересом, а сделанное самими учащимися «открытие» приносит им эмоциональное удовлетворение и гораздо прочнее закрепляется в их памяти, чем знания преподнесенные в «готовом» виде. Эта активная самостоятельная мыслительная деятельность приводит к формированию новых связей, свойств личности, положительных качеств ума и тем самым — к микросдвигу в их умственном развитии (Н. А. Менчинская, А. М. Матюшкин).

Выбор задач для проблемного обучения прежде всего зависит от специфики их содержания. Материал описательного характера, подлежащий усвоению, вряд ли может служит средством проблемного обучения. Проблемными могут стать задачи на применение уже известных закономерностей в относительно новых условиях, но таких, которые предполагают более или менее значительную перестройку знакомых способов решения, выбор из многих возможных вариантов наиболее рационального способа действия, применение общих теоретических положений, принципов решений в реальных практических условиях, требующих внесения в них конструктивных изменений, и т. д. (таких задач немало в производственной деятельности человека) (Т. В. Кудрявцев).

Наибольший эффект при проблемном обучении дают задачи, предполагающие открытие новых для учащихся причинно-следственных связей, закономерностей, общих признаков решения целого класса задач, в основе которых лежат еще не известные субъекту отношения между определенными компонентами исследуемых конкретных ситуаций.

Выбор задачи-проблемы зависит и от наличия у школьников исходного минимума знаний (включая и их операторную сторону) или возможности за относительно короткий срок до постановки проблемы ознакомить учащихся с необходимыми для самостоятельного решения сведениями. Вместе с тем надо помнить, что эти знания должны служить опорой для поисков пути решения, а не «наводить», не подсказывать этот путь, иначе задача перестанет быть проблемной.

Степень сложности задачи, как об этом пишет А. М. Матюшкин, определяется числом существенных взаимосвязей в ее условии, числом опосредований и преобразований, приводящих к нахождению искомого. Зависит она и от уровня самостоятельности при постановке и решении проблемы (В. А. Крутецкий). Наименьшая самостоя­тельность требуется от учащихся тогда, когда преподаватель сам ставит проблему и намечает основные вехи для ее решения, включая школьников лишь в отдельные звенья рассуждения, приводящего к определению искомого. Обычно так идет урок проблемного типа на начальном этапе работы над принципиально новым для школьников разделом программы, когда базис для решения такого рода проблем у них еще очень мал. Поставив проблему, учитель должен дать школьникам самим попытаться ее решить на основе имеющихся знаний и убедиться, что этих знаний для достижения цели явно недостает, а затем принять участие в построении доступных для них звеньев рассуждения, приводящих к новому знанию.

По мере накопления исходных знаний степень самостоятельности поисков решения должна нарастать. Учитель, поставив проблему, предоставляет школьникам самим искать путь ее решения, давая теперь лишь самые общие указания о направлении поиска. Далее он только ставит проблему и ограничивается критикой ложных ходов мысли при попытках школьников найти решение. Наконец, когда у школьников в изучаемой области накопились необходимые знания и навыки, следует предоставить им возможность самим увидеть в предполагаемых исходных ситуациях новую для себя проблему, сформулировать ее и найти способ решения, а педагог лишь в крайнем случае, если сами учащиеся в рассуждениях зашли в тупик, оказывает им минимальную помощь, намекая, как можно выйти из него.

Таковы некоторые более внешние, поддающиеся объективной оценке условия, определяющие проблемность задач. Однако следует особо подчеркнуть, что даже полностью отвечающая указанным условиям задача может не стать для школьников проблемной, если при ознакомлении с ней учителю не удастся создать у них «проблемной ситуации» (А. М. Матюшкин). Проблемная ситуация отражает субъективное принятие задачи, реальное участие каждого школьника (хотя бы мысленно) в процессе ее решения. Важно, чтобы ученик сам задумался над сформулированной в классе проблемой, сам себе задал тот же вопрос и попытался дать на него ответ.

Наиболее эффективное средства для создания у школьников проблемных ситуаций — использование противоречий, конфликта между усвоенными знаниями, знакомыми способами решения определенного класса задач и теми требованиями, которые предъявляет новая задача; школьники должны убедиться в том, что решение задач на основе уже имеющихся знаний приводит к ошибкам. Учитель сознательно заостряет конфликт, подчеркивает возникающее противоречие, стимулирует попытки найти выход из создавшегося положения, разрешить противоречие.

Проблемные ситуации у школьников могут быть созданы тем, что в задачах с недостающими и избыточными данными им будет предложено найти ряд возможных вариантов решения и обоснованно выбрать наиболее эффективный; часть данных в них определяется по таблицам, на основе дополнительных измерений и т. д. Решение таких задач приближает школьное обучение к жизненной практике, повышает действенность знаний, поскольку последние приобретены в процессе более или менее самостоятельной активной мыслительной деятельности.

Конфликтные ситуации, используемые в проблемном обучении, как бы наталкивают учащихся на ошибки. Это противоречит долгое время господствовавшему в методической литературе положению о необходимости оберегать школьников от ошибок. В проблемном обучении при создании конфликтных ситуаций обычно используется материал, в основе усвоения которого лежит углубленное понимание основных отношений между его существенными признаками, закономерностей, общих принципов решения целого класса задач и т. д. Задачи-проблемы ставят ученика в условия неопределенности, и возникновение здесь ошибок вполне возможно. Такие ошибки не страшны, если преподаватель обратит на них внимание школьников и добьется понимания тех причин, которые породили ошибки, и способов их преодоления.

Основной путь открытия нового для человека способа решения проблем — «анализ через синтез» (С. Л. Рубинштейн). Он предполагает включение содержащихся в условии задачи основных и выводимых из них промежуточных данных во все новые и новые системы связей, благодаря чему в них выявляются не выделенные ранее свойства, отношения, раскрываются их возможности для достижения цели.

Возникнет ли в условиях обучения у того или иного учащегося проблемная ситуация, обратиться ли он для ее решения к наиболее эффективному приему продуктивного мышления — «анализ через синтез» или же к механической манипуляции данными — зависит не только от объективных факторов, но и от факторов субъективных, и прежде всего — от умственного развития школьников. Поскольку школьники одного и того же возраста имеют весьма существенные различия в достигнутом ими уровне умственного развития, полная реализация принципа проблемности не может быть осуществлена без индивидуализации обучения.

Умственное развитие составляют как знания (включая и приемы, методы познания), так и обучаемость, способность приобретать эти знания.

Как показали многочисленные эксперименты, весьма существенны индивидуальные различия в уровне усвоения знаний. Школьники, находящиеся в идентичных условиях обучения, усваивают новый для них материал по-разному: одни на высоком, другие на среднем, третьи на низком уровне. При этом показатель уровня усвоения, характерный для того или иного учащегося, довольно устойчив (колебания хотя и имеют место, но обычно в пределах ближайшего уровня). В уровнях усвоения знаний проявляются типичные для учащихся устойчивые особенности психики, от которых зависит успешность учебной деятельности, возможность решать проблемы, требующие предусмотренных программой знаний. Школьники, усвоившие эти знания на низком уровне, не смогут их использовать при решении таких проблем.

Возможно ли доведение каждого учащегося массовой школы до высшего уровня овладения определенными знаниями?

Эксперименты показали, что возможно достижение высшего уровня овладения новым для них понятием всеми учениками, но различным путем. Одни достигают этого уровня уже на основе первичного знакомства с новым для них понятием; для других требуется в среднем решение от 10 до 20 задач с опорой при затруднении на помощь экспериментатора. Третьим необходимо было решить около сотни задач для полного овладения новым для них понятием.

Таким образом, в условиях индивидуализации обучения различия в уровнях знаний (по тому или иному разделу программы) могут быть сняты. В массовой школе, где обычно нет реального учета индивидуальных различий, к концу изучения определенного раздела программы разница в уровнях его усвоения несколько сглаживается, но все же остается весьма значительной.

В еще большей мере, чем от уровня знаний, продуктивность самостоятельной деятельности учащихся при усвоении новых знаний зависит от обучаемости. Среди учащихся разных возрастов имеются школьники с высоким, средним и низким уровнем развития их как практического, так и словесно-логического компонентов продуктив­ного мышления, практики с относительным преобладанием интуитивно-логического мышления над словесно-логическим и небольшое число теоретиков.

Исследования показали, что индивидуально-типические особен­ности развития продуктивного мышления школьников значительно перекрывают возрастные.

В условиях ориентации на «среднего» ученика, т. е. без реальной индивидуализации обучения, замедляется темп развития тех, кто пришел в школу значительно более развитым, чем их сверстники. Но в особенно тяжелые условия попадают школьники с замедленным темпом умственного развития. Условия обучения в массовой школе настолько не соответствуют их возможностям, что такие учащиеся с возрастом не приближаются в своем развитии к сверстникам, а все больше и больше отстают от них.

На успешность учебной деятельности, связанной с продвижением в развитии, большое влияние оказывают и другие стороны психики учащихся, и прежде всего — их умственная работоспособность, которая может в некоторой степени компенсировать наличие относительно невысокой общей успеваемости.

На продуктивность мыслительной деятельности весьма существенно влияет такое качество личности как интеллектуальная активность, или, по терминологии Д. Б. Богоявленской, интеллек­туальная инициатива. Как показали исследования Д. Б. Богоявлен­ской, наличие высоких умственных способностей еще не гарантирует проявление высокого уровня инициативы; нередко весьма способные люди ограничиваются и удовлетворяются решением той или иной поставленной проблемы более элементарным способом, хотя, при соответствующем побуждении со стороны, решают ту же проблему на самом высоком уровне.

Нельзя не учитывать при работе со школьниками и значительных различий в их интересах: от полного отсутствия, до наличия глубокого, устойчивого, разностороннего, активного познавательного интереса к тому или иному изучаемому в школе предмету или к их группе. Существенное влияние на успешность и специфику учебной деятельности оказывают и индивидуальные различия в ее мотивации.

Реально в любом классе нет даже двух учащихся, идентичных друг другу по особенностям своей психики; каждый по своему усваивает учебный материал. Естественно, возникает мысль о том, что в условиях массового обучения принцип его индивидуализации не может быть реализован. Однако это не так. Л. К. Таракановой экспериментально доказана не только возможность, но и высокая эффективность реализации в школе принципа проблемно-индивидуального обучения. При такой форме работы, более развитые школьники имеют возможность работать над материалом повышенной трудности, самостоятельно решать адекватные их возможностям проблемы. Менее развитые получают более подробные объяснения от учителя, решают задачи постепенно повышающейся трудности и, преодолевая трудности с некоторой помощью со стороны, усваивают новый материал, продвигаются в своем развитии, нередко переходя в группы с более высоким уровнем.

Проблемность и другие принципы развития творческого мышления не могут быть реализованы без учета возрастных и индивидуально-типических особенностей мышления. Возрастным особенностям интеллектуального развития посвящено немало исследований. В них выявлена стадиальность развития интеллекта, дана характеристика каждой стадии в зависимости от ведущего вида мыслительной деятельности.

На первой стадии ведущим является наглядно-действенное, практическое мышление, которое осуществляется в конкретной ситуации, в процессе практических действий с реальными предметами. У маленьких детей это «мышление руками». Малыш тянется к игрушке, не может её достать и после ряда попыток использует палку или лезет на табуретку, чтобы получить заинтересовавший его предмет.

На второй стадии преобладает наглядно-образное мышление; оно позволяет решать задачи на основе оперирования уже не реальными предметами, а образами восприятия и представлений, содержащимися в детском опыте. Связь мышления с практическими действиями хоть и сохраняется, но не является такой прямой, непосредственной, как раньше. чтобы решать задачи ребенок должен отчетливо воспринимать, наглядно представлять рисуемую в них ситуацию.

На третьей, высшей, ступени развития ведущую роль в мыслительной деятельности приобретает отвлеченное, абстрактно-теоретическое мышление. Мышление выступает здесь в форме отвлеченных понятий и рассуждений, отражающих существенные стороны окружающей действительности, закономерные связи между ними. Овладение в ходе усвоения основ наук понятиями, законами, теориями оказывает значительное влияние на умственное развитие школьников. Оно раскрывает богатые возможности самостоятельного творческого приобретения знаний, их широкого применения на практике.

Полученная в исследованиях характеристика стадий мышления позволила наметить основную линию его развития — от практического мышления, скованного конкретной ситуацией, к отвлеченному абстрактно-теоретическому мышлению, безгранично расширяющему сферу познания, позволяющему выходить далеко за пределы непосредственного чувственного опыта.

Под влиянием всевозрастающих требований к школьному образованию психологи начали исследовать «зону ближайшего развития» детей. Была поставлена задача выяснить, каковы возможности мышления детей, если так изменить содержание и методы обучения, чтобы они активизировали развитие отвлеченного, абстрактно-теоретического мышления (В. В. Давыдов, С. Ф. Жуйков, Л. В. Занков, А. В. Запорожец, А. А. Люблинская, Н. А. Менчинская, А. В. Скрипченко, Д. Б. Эльконин и др.).

Эксперименты блестяще подтвердили гипотезу о гораздо больших, чем считалось ранее, возможностях интеллекта детей. Оказалось, что уже первоклассники могут оперировать отвлеченными символами, решать задачи на основе формул, овладевать грамматическими понятиями и т. д.

Вместе с тем установка на более раннее развитие отвлеченного, понятийного мышления, на его формировании на основе движения «от абстрактного к конкретному» — вероятно, вследствие подчас ошибочного понимания сущности этого процесса — на практике нередко приводит к недооценке роли наглядности, конкретизации знаний, а также к значения деятельности и других видов мышления. Нельзя забывать о том, что и отвлеченное, абстрактно-теоретическое мышление, далеко выходя за пределы чувственного опыта, только тогда обладает действенной силой, позволяет проникать в суть познаваемой действительности, когда оно неразрывно связано с наглядно-чувственными данными. Форсированное развитие отвлеченного мышления, без достаточной конкретизации усваиваемого материала, без связи с наглядно-практическим и наглядно-образным мышлением может привести к формальному усвоению знаний, к образованию пустых абстракций, оторванных от живой действительности.

Гармоничное развитие личности предполагает активизацию всех видов мышления, их совершенствование.

Необходимость развивать различные виды мыслительной деятельности вытекает из специфики продуктивного, творческого мышления. Процесс открытия новых знаний и у ребенка, впервые познающего давно открытые человечеством истины, и у ученого, впервые проникающего за пределы известного, не происходят в виде строгих логических рассуждений, непосредственно опирающихся на знакомые закономерности. Решение проблемы нередко происходит интуитивно, и в этом процессе существенную роль играют и практическое и образное мышление, непосредственно связанное с чувственной опорой.

Решение проблемы в словесном плане, на основе теоретических рассуждений развертывается постепенно, звено за звеном. человеку невозможно при этом охватить все необходимые звенья, что затрудняет установление взаимосвязи между ними. Включение в этот процесс наглядно-образного мышления дает возможность сразу, «одним взглядом» охватить все входящие в проблемную ситуацию компоненты, а практические действия позволяют установить взаимосвязь между ними, раскрыть динамику исследуемого явления и тем самым облегчают поиск решения.

Преобладание практических, образных или понятийных видов мыслительной деятельности определяется не только спецификой решаемой проблемы, но и индивидуальными особенностями самих людей.

Вот почему мы полагаем, что одним из важнейших принципов развития творческого мышления является оптимальное (отвечающее целям обучения и психическим особенностям индивида) развитие разных видов мыслительной деятельности: и абстрактно-теоретического, и наглядно-образного, и наглядно-действенного, практического мышления.

Исследование процесса усвоения и применения знаний показали, что обычно учащиеся усваивают содержательную сторону знаний и непосредственно с ней связанные конкретные приемы решения довольно узкого круга задач. Лишь у школьников с высокой обучаемостью на основе решения единичных задач формируются обобщенные приемы, методы решения целого класса задач. Формирование такого рода обобщенных приемов умственной деятельности чрезвычайно важно, так как оно означает существенный сдвиг в интеллектуальном развитии, расширяет возможности переноса знаний в относительно новые условия. Поскольку основная масса учащихся самостоятельно не овладевает более обобщенными приемами умственной деятельности, их формирование должно стать важной задачей обучения.

В соответствие с этим одним из принципов развития творческого, продуктивного мышления является специальное формирование обобщенных приемов умственной деятельности.

Обобщенные приемы умственной деятельности делятся на две большие группы — приемы алгоритмического типа и эвристические.

Остановимся сначала на характеристике приемов алгоритмического типа.

Это приемы рационального, правильного мышления, полностью соответствующего законам формальной логики. Точное следование предписаниям, даваемым такими приемами, обеспечивает безошибочное решение широкого класса задач, на который эти приемы непосредственно рассчитаны.

Вооружение учащихся правильными, рациональными приемами мышления, обучение тому, как определять понятия, классифицировать их, строить умозаключения, решать в соответствии с данным алгоритмом задачи, оказывает положительное влияние и на самостоятельное, продуктивное мышление, обеспечивает возможность решения задач-проблем.

Формирование приемов мыслительной деятельности алгоритмического типа, ориентирующих на формально-логический анализ задач, является необходимым, но не достаточным условием развития мышления. Необходимо оно, во-первых, потому, что содействует совершенствованию репродуктивного мышления, являющегося важным компонентом творческой деятельности (особенно на начальном и конечном этапах решения проблем). Во-вторых, эти приемы служат тем фондом знаний, из которых ученик может черпать «строительный материал» для создания, конструирования методов решения новых для него задач. Недостаточным формирование алгоритмических приемов является потому, что не соответствует специфике продуктивного мышления, не стимулирует интенсивное развитие именно этой стороны мыслительной деятельности.

Вот почему формирование таких приемов должно сочетаться со специальным вооружением учащихся приемами эвристического типа.

Приемы другого типа назвали эвристическими потому, что они непосредственно стимулируют поиск решения новых проблем, открытие новых проблем, открытие новых для субъекта знаний и тем самым соответствуют самой природе, специфике творческого мышления. В отличии от приемов алгоритмического типа, эвристические приемы ориентируют не на формально-логический, а на содержательный анализ проблем. Они направляют мысль решающих на проникновение в суть описываемого в условии предметного содержания, на то, чтобы за каждым словом они видели его реальное содержание и по нему судили о роли в решении того или иного данного. Многие эвристические приемы стимулируют включение в процесс решения проблем наглядно-образного мышления, что позволяет использовать его преимущество перед словесно логическим мышлением — возможность целостного восприятия, видения всей описываемой в условии ситуации. Тем самым облегчается течение характерных для продуктивного мышления интуитивных процессов.

Часть этих приемов направляет решающего на использование весьма характерного для творческой деятельности мыслительного эксперимента, который облегчает постановку и предварительную проверку гипотез и пути решения проблем. Включая имеющиеся в условии задачи данные в различные связи, в новые ситуации, решающий тем самым «вычерпывает» их новые признаки, используя оптимальный для творческого процесса «анализ через синтез».

К эвристическим приемам относится конкретизация, когда ученик придает абстрактным данным условия более конкретную форму. Так, в задаче сказан, что при продаже товара получено 1260 рублей прибыли. Ученик уточняет: «Это магазин купил за какую-то цену, а потом продал товар и за него получил на 1260 рублей больше». Этот прием дополняется приемом графического анализа, вводящего наглядные опоры различной степени символизации. Например, к той же задаче испытуемый набрасывает схему, отражающую «надбавку»:

Противоположным является прием абстрагирования, когда решающий отбрасывает конкретные детали, «оголяя» данные и соотношения между ними. «На 4800 рублей больше и вдвое дороже» — вот и все, что выделено учеником в одной из задач, и на этом сосредотачивает он внимание.

Наиболее распространенным приемом, облегчающим выявление функциональных связей между данными, является варьирование. Этот прием заключается в том, что ученик произвольно отбрасывает или изменяет величину одного из данных (а иногда и нескольких) и на основе логического рассуждения выясняет, какие следствия вытекают из такого преобразования, как отразилась изоляция данного на остальных. По этим изменениям легче судить о связи выделенного данного с другими. Например, в одной из задач испытуемый последовательно отбрасывает содержащиеся в ней данные. «Если отбросить 1 руб. 50 коп., т. е. разницу между литра кислоты и литра раствора, то стало бы дешевле… А у нас получено 3 рубля прибыли… Забудем о трех рублях…» Решающий отбрасывает три рубля, потом пять литров воды, добавленные в кислоту, и это последовательное мысленное экспериментирование приводит его к верному решению.

Широко используются при решении проблем приемы аналогии, постановка аналитических вопросов.

Проблеме эвристических приемов решения задач посвящена книга Д. Пайя «Как решать задачу». Автор рекомендует прежде всего хорошо понять условие задачи, последовательно ставя себе вопросы: «Что известно? Что дано? Достаточно ли этих данных, чтобы определить искомое?» И т. п. Далее он советует сделать чертеж, кратко записать условие, разбить его на части. Полезно вспомнить похожую задачу и попробовать использовать метод её решения или же применить аналогию.

Владеют ли эвристическими приемами школьники и с какого примерно возраста? Как они ими овладевают? Исследования показывают, что эти приемы при решении новых задач используют лишь наиболее развитые школьники.

Очевидно, необходимо специально обучать эвристическим приемам.

Имеются работы, направленные на решение этой задачи. Такое исследование, например, проведено Ю. Н. Кулюткиным. В нем были использованы элементы программированного обучения, составлены программы, предусматривающие описание эвристических приемов. К ним относятся следующие приемы:

Первоначальная схематизация имеющихся в условии задачи отношений (т. е. краткое её содержание с выделением исходных данных).

Перевод условия с житейского языка, на котором оно нередко дано, на язык научных терминов, понятий.

Привлечение наглядности, в том числе наглядных аналогий, как опоры для поиска решения.

Условное упрощение анализируемой системы.

Уточнение идеи решения, когда она найдена (т. е. точное определение того типа соотношений, которое содержится в данной ситуации).

Ю. Н. Кулюткин указывает, что положительным итогом проведенного обучения явилось изменение самого подхода к учению. Школьников стала привлекать самостоятельная познавательная деятельность, т. е. у них изменилась мотивация учения. Очевидно, существенное влияние оказали положительные эмоции, возникающие при самостоятельном открытии, которое оценивается решающим, как его интеллектуальная победа.

Итак, алгоритмические приемы обеспечивают правильное решение задач известных учащимся типов; они учат школьников логике рассуждений, служат фоном, который возможно использовать при поисках решения проблем. Эвристические приемы позволяют действовать в условиях неопределенности, в принципиально новых ситуациях, облегчая поиск решения новых проблем.

Следовательно одним из принципов развития творческого мышления должно быть специальное формирование как алгоритмических, так и эвристических приемов умственной деятельности.

В психологических работах, непосредственно связанных с проблемами продуктивного, творческого мышления, немалое внимание уделяется описанию отрицательной роли прошлого опыта, который может препятствовать, тормозить движение в принципиально новом направлении, подчеркивается необходимость преодоления «барьера прошлого опыта».

Эти исследования отражают известный прогресс в решении проблемы продуктивного мышления и путей его развития и оказывают свое положительное влияние на практику обучения. Однако, как это нередко бывает, усиленное внимание к одной стороне мыслительной деятельности (продуктивному мышлению) в практике обучения может привести к недооценке другой ее стороны — репродуктивного мышления и неразрывно связанной с ней мнемической деятельности, обеспечивающей прочность знаний, их готовность к актуализации в соответствии с требованиями задачи. В результате этого у школьников подчас не формируется прочной системы знаний основ изучаемого материала, из-за чего тормозится и интеллектуальное развитие.

Нередко полагают, например, что не следует заботиться о знании формул, их всегда можно воспроизвести по справочникам. Ответ на вопрос, надо ли запоминать формулы, в частности, получен в исследовании С. И. Шапиро. Результаты экспериментов показали, что в простых ситуациях, когда зависимости используются всегда одинаково (т. е. когда требуется репродуктивное мышление), их предварительное специальное запоминание не обязательно, вполне возможно использование внешних средств (справочников и т. п.). Напротив, в сложных ситуациях, при решении нестандартных задач, т. е. тогда, когда должно активизироваться продуктивное мышление, необходимо прочное закрепление основных формул в памяти. Известный педагог В. Ф. Шаталов на аналогичный вопрос отвечает: «Ученик, который работает со справочником, отличается от ученика, который знает все формулы, так же как отличается начинающий шахматист от гроссмейстера. Он видит только один ход вперед.»

Прямая установка на запоминание повышает уровень мыслительной активности при работе над подлежащим усвоению материалом, степень ее саморегуляции и самоконтроля, что значительно увеличивает эффект усвоения. Этому же способствует сознательное применение рациональных приемов мнемической деятельности (таких как группировка, классификация, составление плана, выделение смысловых опор и т. д.). Продуктивное мышление предполагает выход за пределы имеющихся знаний. Однако именно эти знания — опора в открытии нового. Чтобы открывать новое, отвергать уже известное, необходимо владеть этим старым, иметь достаточно широкий объем знаний (включая и их операционную сторону), достаточных для движения вперед и находящихся в состоянии готовности к актуализации в соответствии с поставленной перед субъектом целью. Чтобы выполнить это чрезвычайно важное требование, нужно предусмотреть специ­альную организацию мнемической деятельности, обеспечивающую прочность усваиваемых знаний и их готовность к актуализации при решении проблем. Эта специальная организация — один из важнейших принципов развития продуктивного мышления.

Для обеспечения достаточного уровня знаний авторы учебных программ и учебников стремятся вводить в них все новые и новые данные. Однако, чем больше объем подлежащих усвоению знаний, тем труднее обеспечить прочность их усвоения. Следовательно, необходимо как-то ограничить тот круг знаний, которые подлежат усвоению и искать пути организации знаний в такую систему высокого уровня обобщения, в которой по относительно немногим прочно закрепленным ее звеньям на основе рассуждений ученик мог бы найти дополнительные звенья, необходимые для оперирования приобретенными знаниями.

Важно четко ограничить обязательный минимум знаний от второстепенного материала и ориентировать учащихся на тщательное закрепление именно основных знаний и способов оперирования ими, что лучше делать сразу же при введении нового материала.

Ориентация на выделение и обобщение существенного в материале, классификацию в зависимости от его значимости содействует формированию одного из важнейших качеств продуктив­ного мышления — глубины ума.

В связи с большим объемом подлежащих усвоению знаний необходимо по возможности «сжать», «уплотнить» их, что может быть осуществлено на основе более раннего введения обобщенных знаний — теорий, законов, общих методов решения широкого класса задач. Такие знания позволяют учащимся не запоминать множество отдельных частных закономерностей, способов решения, а самим на основе логических рассуждений «выводить» их из общих положений.

С целью практического обоснования выводов, полученных в ходе наблюдения за деятельностью учащихся седьмых классов средней школы нами было проведено исследование.

Работа велась с октября 1995 по март 1996 гг. и предусматривала несколько этапов.

На первом этапе проводился констатирующий эксперимент, направленный на выяснение уровня сформированности продуктивного мышления.

Вторым этапом работы было проведение серии экспериментальных занятий, направленных на формирование у учащихся рациональных приемов творческой мыслительной деятельности.

Заключительный, третий этап исследования, проводился теми же методами, что и первый. Целью этого этапа было — выявить какие-либо индивидуальные изменения в развитии обучаемости.

Затем следовало подведение итогов исследования. Рассмотрим подробнее каждый из этапов.

В соответствии с целями исследования за основу методики на первом этапе был взят метод Калмыковой З. И. (Калмыкова З. И. Продуктивное мышление как основа обучаемости. М., 1981.).

Нами была проведена модификация этого теста.

В связи с тем, что занятия по экспериментальной программе представилось возможным провести только в двух седьмых классах средней школы № 18, тестирование было проведено в трех классах: двух «экспериментальных» (52 чел.) и «контрольном» (28 чел.), т. е. в нем участвовало 80 человек.

В нашей методике моделировалось проблемное обучение, непосредственно направленное на развитие продуктивного мышления. Она была построена в виде естественного обучающего эксперимента, в котором школьники включаются в проблемные ситуации, рассчитанные на самостоятельное решение новых для них учебных задач.

В качестве задачи-проблемы в методике была использована известная физическая закономерность, отражающая условия равновесия рычага. Для ее решения учащиеся располагают необходимыми знаниями. Они не раз встречались с простейшими случаями равновесия — взвешивание на рычажных весах, качание на доске с опорой и т. д. Кроме того, в эксперименте использовалась хорошая модель (демонстрационный рычаг), которая служила наглядной опорой при “открытии” учащимися закономерности. Преимущества данной закономерности в том, что она может быть показана на ряде моделей (рычаг с опорой между линиями действия сил, ворот и т. д.). тем самым есть возможность создать варианты методики, необходимые при повторных испытаниях, что важно для суждения об индивидуальных сдвигах в развитии обучаемости.

Остановимся кратко на характеристике структуры экспериментов и способов обработки получаемых на их основе данных.

Эксперимент включал три этапа: предварительный, основной и вспомогательный. На предварительном этапе экспериментатор обеспечивал школьникам исходный минимум знаний; создавалась установка на решение новой проблемы, вызывалось желание решить ее как можно лучше, без боязни ошибиться при поисках решения. С этой целью на ряде простых арифметических задач экспериментатор напоминал школьникам в (практическом плане) о прямой и обратной зависимости. Далее им говорили, что в связи с работой над новыми вариантами хотят выяснить, возможно ли с учащимися VII класса решать задачи, которые ранее решались только старшеклассниками.

Благодаря такой мотивировке, школьники считали себя участниками эксперимента, не имеющего прямого отношения к их собственным способностям. Если школьник затруднялся в решении, то это ему объясняли трудностью решения задач для данного возраста.

После такой подготовке переходили к основному этапу эксперимента. Учащемуся показывали рычаг, его плечи и силы (гири по 100 г). Экспериментатор говорил школьнику, что тот должен решить ряд практических задач, в которых по величинам сил и плеч догадаться, будет ли рычаг в равновесии. Пользуясь моделью рычага или посмотрев ответ на обороте карточки, он мог проверить, верна ли его догадка. После решения ряда задач ему следовало ответить на более общий вопрос: при каких условиях рычаг в равновесии, то есть самому “открыть” неизвестную ему закономерность, на основе которой можно безошибочно решать такие задачи.

Затем экспериментатор клал перед испытуемыми карточки с записанными на них величинами сил и плеч.

Всего испытуемый практически решал 30 задач, разделенных на 6 циклов. Нечетные циклы имели по 4 задачи, а четные — по 6. Нечетные циклы получили название наглядно-действенных, так как в них от ученика, требовалось сделать заключение об условиях равновесия рычага на основе практических действий с реальной моделью рычага. Получив карточку с условием задач, школьник в соответствии с ним вешал гирьки (каждая по 100 г) на указанном расстоянии от опоры. Экспериментатор в это время удерживал рычаг в равновесии. Учащийся высказывал свое предположение о том, будет ли рычаг в равновесии, после чего экспериментатор отпускал рычаг и учащийся мог проверить правильность своего предположения. Четные циклы названы числовыми, так как в них учащийся имел дело только с числовыми данными, сопоставляя которые он высказывал свою гипотезу о наличии или отсутствии равновесия, а проверял ее по ответу на обороте карточки.

Содержание всех 30 задач было идентичным, изменялись лишь числовые данные. Последние подбирались так, чтобы операции с ними не вызывали никаких трудностей.

После решения задач каждого из 6 циклов школьнику предлагалось попытаться сформулировать искомую закономерность, то есть ответить на вопрос: при каких условиях рычаг будет в равновесии? На основном этапе задачи решались самостоятельно, а подкреплением служило лишь сопоставление гипотезы испытуемого о наличии равновесия с верным ответом. Каждый испытуемый, вне зависимости от правильности ответов решал все 30 задач.

Вспомогательный этап экспериментов рассчитан только на тех, кто на основном этапе не решил проблему, то есть не дал верную формулировку условий равновесия рычага. Его цель — определить меру помощи, которая требуется для решения проблемы.

Остановимся теперь на характеристике тех показателей, по которым мы судили при анализе собранного экспериментального материала о продуктивности мышления школьников давая его качественную характеристику.

Самостоятельность ума мы определяли по тому, справился ли школьник с решением проблемы на основном этапе экспериментов, или ему потребовалась дополнительная помощь, предусмотренная на вспомогательном этапе, и какая именно. Было предусмотрено 4 степени помощи, от минимальной к максимальной.

По степени помощи, необходимой испытуемому для выделения искомой закономерности (условия равновесия рычага) определяли потенциальные возможности учащегося в решении проблемы.

Глубина ума, отражающая степень существенности абстрагируемых признаков и степени их обобщенности, определялась на основе анализа суждений испытуемых при их попытках сформулировать искомую закономерность.

Об осознанности мыслительной деятельности и характере ее реализации можно судить по соотношению хода практического решения задач с высказывании испытуемых о тех признаках, по которым, по их мнению, они определяли наличие или отсутствие равновесия. Отсутствие соответствия между ними дает основание для утверждения о слабой осознанности мыслительной деятельности, о преобладании интуитивно-практического мышления над словесно-логическим; их соответствие говорит об осознанности этой деятельности.

Гибкость ума проявляется в возможности формулировки двух вариантов искомой закономерности (по пропорциональности величин сил и плеч, и по моменту сил), в совершенствовании раз сформулированного суждения, в переходе к суждениям более высокой степени обобщенности, введении в них новых научных терминов вместо житейских, в легкости отказа от ошибочности суждений и т. д.

Устойчивость ума найдет свое выражение в воспроизведении и целесообразной ориентации на найденный в процессе анализа значимый признак равновесия, в возможности одновременной ориентации на оба признака равновесия.

Определяющее условие количественной оценки результатов экспериментов исследуемой стороны мышления — адекватность этой оценке, качественной ее характеристике.

Качественный анализ продуктивного мышления школьников привел к выводу, что наиболее общим, суммарным показателем уровня его развития может служить экономичность мышления, как краткость пути к самостоятельному решению проблемы.

В определении показателя экономичности мышления при решении проблемы мы исходим из следующей гипотезы: чем раньше испытуемый выделит существенные признаки равновесия и будет ориентироваться на них, тем вернее он будет решать задачи. Следовательно, об уровне экономичности можно судить по совокупности баллов, начисленных за верно решенные задачи.

Показатели экономичности мышления располагались в интервале от 0 до 1, мы выделили три их уровня (на основе простого деления общего интервала на 3).

К низшему уровню были отнесены показатели от 0 до 0,33; к среднему от 0,34 до 0,67; к высшему от 0,68 до 1,00.

В ходе проведения эксперимента были получены следующие результаты. 18 человек (35%) «экспериментальных» классов (классов, в которых в дальнейшем велись занятия по математике по экспериментальной методике) показали достаточно высокие результаты и были отнесены нами к высшему уровню экономичности мышления. По такому же принципу в «контрольном» классе к высшему уровню экономичности мышления были отнесены 10 учащихся (36%). Большая часть испытуемых из всех классов была отнесена нами к среднему уровню: 26 человек из «экспериментальных» классов и 14 из «контрольного»; или соответственно 50% и 50%. Наконец, по 4 человека из каждого класса были отнесены нами к низшему уровню показателя экономичности мышления (15% и 14% соответственно).

Следовательно, исходя из вышеперечисленных данных общий уровень экономичности мышления можно считать достаточно высоким. При этом мы допускаем наличие возможных погрешностей в исполнении, обработке и трактовке данных.

Кроме того, сравнение результатов учащихся трех седьмых классов (так называемых «экспериментальных» и «контрольного») делает допустимым проведение в двух из них занятий по экспериментальной методике и проведение в дальнейшем повторных испытаний с целью выяснить влияние экспериментальной обучающей методики на развитие продуктивного мышления учащихся.

Следующим этапом нашей работы было проведение серии экспериментальных занятий с учащимися 7-х классов средней школы г. Астрахани.

Мы не приводим в нашей работе описание каждого проведенного урока. Останавливаемся лишь на некоторых методических приемах, использовавшихся нами на уроках алгебры для активизации творческой мыслительной деятельности учащихся, и их теоретическом обосновании.

Мы считаем, что развитие творческого мышления у учащихся в процессе изучения ими математики является одной из актуальных задач, стоящих перед преподавателями математики в современной школе. Основным средством такого воспитания и развития математических способностей учащихся являются задачи. Не случайно известный современный математик и методист Д. Пойа пишет: “Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности”.

При обучении математике на решение задач отводиться бульшая часть учебного времени. Отсюда напрашивается вывод, что учебное время, отводимое на решение задач в школе, используется неэффективно, а это отрицательно сказывается на качестве обучения математике в целом.

Одна из главных причин затруднений учащихся, испытываемых ими при решении задач, заключается в том, что математические задачи, содержащиеся в основных разделах школьных учебников, как правило, ограничены одной темой. Их решение требует от учащихся знаний, умений и навыков по какому-нибудь одному вопросу программного материала и не предусматривает широких связей между различными разделами школьного курса математики. Роль и значение таких задач исчерпываются в течении того непродолжительного периода, который отводиться на изучение (повторение) того или иного вопроса программы. Функция таких задач чаще всего сводиться к иллюстрации изучаемого теоретического материала, к разъяснению его смысла. Поэтому учащимся нетрудно найти метод решения данной задачи. Этот метод иногда подсказывается названием раздела учебника или задачника, темой, изучаемой на уроке, указаниями учителя и т. д. Самостоятельный поиск метода решения учеником здесь минимален. При решении задач на повторение, требующих знания нескольких тем, у учащихся, как правило, возникают определенные трудности.

К сожалению, в практике обучения математике решение задач чаще всего рассматривается лишь как средство сознательного усвоения школьниками программного материала. И даже задачи повышенной трудности специальных сборников, предназначенных для внеклассной работы, в основном имеют целью закрепление умений и навыков учащихся в решении стандартных задач, задач определенного типа. А между тем функции задач очень разнообразны: обучающие, развивающие, воспитывающие, контролирующие.

Каждая предлагаемая для решения учащимся задача может служить многим конкретным целям обучения. И все же главная цель задач — развить творческое мышление учащихся, заинтересовать их математикой, привести к “открытию” математических фактов.

Достичь этой цели с помощью одних стандартных задач невозможно, хотя стандартные задачи, безусловно, полезны и необходимы, если они даны вовремя и в нужном количестве. Мы считаем, что следует избегать большого числа стандартных задач как на уроке, так и во внеклассной работе, так как в этом случае сильные ученики могут потерять интерес к математике и даже испытать отвращение к ней.

Ознакомление учащихся лишь со специальными способами решения отдельных типов задач создают, на наш взгляд, реальную опасность того, что учащиеся ограничатся усвоением одних шаблонных приемов и не приобретут умения самостоятельно решать незнакомые задачи (“Мы такие задачи не решали”,— часто заявляют учащиеся, встретившись с задачей незнакомого типа).

В системе задач школьного курса математики, безусловно, необходимы задачи, направленные на отработку того или иного математического навыка, задачи иллюстративного характера, тренировочные упражнения, выполняемые по образцу.

Но не менее необходимы задачи, направленные на воспитание у учащихся устойчивого интереса к изучению математики, творческого отношения к учебной деятельности математического характера. Необходимы специальные упражнения для обучения школьников способам самостоятельной деятельности, общим приемам решения задач, для овладения ими методами научного познания реальной действительности и приемам продуктивной умственной деятельности, которыми пользуются ученые-математики, решая ту или иную задачу.

Осуществляя целенаправленное обучение школьников решению задач, с помощью специально подобранных упражнений, можно учить их наблюдать, пользоваться аналогией, индукцией, сравнениями, и делать соответствующие выводы. Необходимо, как мы считаем, прививать учащимся прочные навыки творческого мышления.

В школьных учебниках математики (и не только ныне действующих) мало задач, с помощью которых можно показать учащимся роль наблюдения, аналогии, индукции, эксперимента.

Мы исходим из того, что несмотря на ошибочные гипотезы, которые можно получить в результате наблюдений и неполной индукции, учитель должен использовать все предоставляемые ему программой и учебниками (в том числе и ранее действующими, и пробными, экспериментальными) возможности, чтобы развить у учащихся навыки творческого мышления. С этой целью, например, мы предлагали учащимся следующую задачу: “Может ли: а) сумма пяти последовательных натуральных чисел быть простым числом; б) сумма квадратов пяти последовательных натуральных чисел быть простым числом?” ((3), №1168).

Иногда для развития навыков творческого мышления мы посчитали нужным несколько изменять условия задач, встречающихся в школьных и других учебниках.

Перед решением задачи “Доказать, что если из трехзначного числа вычесть трехзначное число, записанное теми же цифрами, что и первое, но в обратном порядке, то модуль полученной разности будет делиться на 9 и 11” ((1), № 949) целесообразно для математического развития учащихся предложить им установить (с помощью индукции), каким свойством обладает рассматриваемая разность (делиться на 9, 11, 99), и только после этого доказать подмеченную на частных примерах закономерность в общем виде.

Задача “Докажите, что для того, чтобы найти квадрат двузначного числа, оканчивающегося цифрой 5 и имеющего п десятков достаточно число десятков п умножить на п + 1 и к результату приписать 25” ((4), № 969) безусловно имеет определенную познавательную ценность: учащиеся знакомятся с правилом возведения в квадрат двузначных чисел, оканчивающихся на 5. Но роль этой задачи возрастет, если ее сформулировать так: “Найдите и обоснуйте правило возведения в квадрат двузначных чисел, оканчивающихся на цифрой 5”.

Полезно предложить учащимся VII класса самим установить с помощью наблюдений и индукции следующие формулы для подсчета сумм:

1 + 3 + 5 + … + (2п – 1) = п2,

13 + 23 + 33 + … + п3 = (1 + 2 + 3 + … + п)2.

Учащиеся, не знакомые с методом математический индукции, используемым для доказательства этих формул, именно с помощью такого рода задач понимали необходимость изучения этого метода в дальнейшем.

Приведенные задачи решались со всеми учащимися на уроках, в процессе изучения или повторения программного материала, а не только с отдельными, хорошо успевающими учениками во внеурочное время.

Мы исходим из того, что необходимо на уроках систематически использовать задачи, способствующие целенаправленному развитию творческого мышления учащихся, их математическому развитию, формированию у них познавательного интереса и самостоятельности. Такие задачи требуют от школьников наблюдательности, творчества и оригинальности.

Эффективное развитие математических способностей у учащихся невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических ребусов, софизмов.

Как показали проведенные нами занятия, рассмотрения на уроке математического софизма, для разгадки которого недостаточно известного учащимся материала, вызывает естественный интерес к новой теме, осознание необходимости ее изучения и соответствующий настрой к преодолению предстоящих на пути приобретения новых знаний трудностей.

Какая задача называется нестандартной? “Нестан­дартные задачи — это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения” (Фрид­ман Л. М., Турецкий Е. Н. Как научиться решать задачи.— М.: Просвещение, 1989.— С. 48.).

Однако следует заметить, что понятие “нестандартная задача” является относительным. Одна и та же задача может быть стандартной и нестандартной, в зависимости от того, знаком решающий задачу со способами решения задач такого типа или нет. Например, задача “Представьте выражение 2х2 + 2у2 в виде суммы двух квадратов” ((5), № 1264) является для учащихся нестандартной до тех пор, пока учащиеся не познакомились со способами решения таких задач. Но если после решения этой задачи учащимся предложить несколько аналогичных задач, такие задачи становятся для них стандартными. Аналогично задача “При каких натуральных значениях х и у верно равенство 3х + 7у = 23?” ((5), № 1278) является нестандартной для учащихся VII класса до тех пор, пока учитель не познакомит их со способами решения таких задач (что, кстати сказать, можно сделать при обучении учащихся математике уже в VI классе).

Таким образом, нестандартная задача — это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение.

К сожалению, иногда учителя единственным способом обучения решению задач считают показ способов решения определенных видов задач, после чего следует порой изнурительная практика по овладению ими. Нельзя не согласиться с мнением известного американского математика и методиста Д. Пойа, что, если преподаватель математики “заполнит отведенное ему учебное время натаскиванию учащихся в шаблонных упражнениях, он убьет их интерес, затормозит их умственное развитие и упустит свои возможности”.

Как же помочь учащимся научиться решать нестандартные задачи?

Универсального метода, позволяющего решить любую нестандартную задачу, к сожалению, видимо нет, так как нестандартные задачи в какой-то степени неповторимы. Однако опыт работы многих передовых учителей, добивающихся хороших результатов в математическом развитии учащихся как у нас в стране, так и за рубежом, позволяет сформулировать некоторые методические приемы обучения учащихся способам решения нестандартных задач.

В литературе (отечественной и зарубежной) методические принципы обучения учащихся умением решать нестандартные задачи описаны неплохо. Наиболее удачными, на наш взгляд, в этом отношении являются книги Д. Пойа “Как решать задачу”, “Математическое открытие”, “Математика и правдоподобные рассуждения” Л. М. Фридмана, Е. Н. Турецкого “Как научиться решать задачу”, Ю. М. Колягина, В. А. Оганесяна “Учись решать задачи”. И хотя некоторые из них адресованы учащимся, желающим научиться решать задачи, они, без сомнения, могут быть использовании учителями при обучении школьников умениям решать нестандартные задачи.

Прежде всего отметим, что научить учащихся решать задачи (в том числе и нестандартные) можно только в том случае, если у учащихся будет желание их решать, то есть если задачи будут содержательными и интересными с точки зрения ученика. Поэтому проблема первостепенной важности, стоящая перед учителем,— вызвать у учащихся интерес к решению той или иной задачи. Необходимо тщательно отбирать интересные задачи и делать их привлекательными для учащихся. Как это сделать — решать самому учителю. Наибольший интерес вызывают у учащихся задачи, взятые из окружающей их жизни, задачи, естественным образом связанные со знакомыми учащимся вещами, опытом, служащие понятной ученику цели.

Учитель, как нам кажется, должен уметь находить интересные для учащихся задачи и своевременно предлагать их. Приведем примеры.

Учитель математики обратил внимание учащихся, что в фильме “Возвращение с орбиты”, показанном накануне по телевизору, главный герой, узнав, что его невесте 24 года, говорит ей: “Когда тебе будет столько лет, сколько мне сейчас, мне будет 60”. Вопрос учителя “Сколько лет герою фильма” вызвал у всех учащихся VII—VIII классов желание решить предложенную задачу, хотя от некоторых она потребовала настоящего усилия.

Другой пример. Желая научить учащихся решать в натуральных числах уравнения вида ах + by = с, можно, конечно, предложить учащимся выполнить упражнение № 1278 из (5) (При каких натуральных значениях х и у верно равенство 3х+7у=23?). Но, как показывают наши наблюдения, учащиеся легче и с бульшим интересом учатся способам решения таких уравнений, если им предложить, например, следующую задачу:

“Чтобы купить вещь, нужно уплатить 19 р. У покупателя только трехрублёвые купюры, у кассира только десятирублевые. Может ли покупатель расплатиться за покупку? А если у кассира только пятирублевые купюры?”

Большой интерес, являющийся для учащихся стимулом для приобретения умений и навыков решения неопределенных уравнений первой степени с двумя неизвестными в натуральных и целых числах, вызывает, как правило, у учащихся VII класса следующая задача:

“В комнате стоят стулья и табуретки. У каждой табуретки три ножки, у каждого стула четыре ножки. Когда на всех стульях и табуретках сидят люди, в комнате 39 “ног”. Сколько стульев и табуреток в комнате?” (Если стульев х, табуреток у, то имеем уравнение 4х + 3у + 2 (х + у) = 39, откуда 5у = 39 – 6х, х = 4, у = 3.) Много интересных задач на соответствующую тематику имеется в журнале “Квант”.

Мы понимаем, конечно, что нельзя приучать учащихся решать только те задачи, которые вызывают у них интерес. Но нельзя и забывать, что такие задачи учащийся решает легче и свой интерес к решению одной или нескольких задач он может в дальнейшем перенести и на “скучные” разделы, неизбежные при изучении любого предмета, в том числе и математики.

Таким образом, учитель, желающий научить школьников решать задачи, должен, на наш взгляд, вызвать у них интерес к задаче, убедить, что от решения математической задачи можно получить такое же удовольствие, как от разгадывания кроссворда или ребуса.

Задачи не должны быть слишком легкими, но и не должны быть слишком трудными, так как учащиеся, не решив задачу или не разобравшись в решении, предложенном учителем, могут потерять веру в свои силы. Не следует предлагать учащимся задачу, если нет уверенности, что они смогут ее решить.

Ну а как же помочь учащемуся научиться решать задачи, если интерес к решению задач у него есть и трудности решения его не пугают? В чем должна заключаться помощь учителя ученику, не сумевшего решить интересную для него задачу? Как эффективным образом направить усилия ученика, затрудняющегося самостоятельно начать или продолжить решение задачи?

Мы считаем, что не следует идти по самому легкому в этом случае пути — познакомить ученика с готовым решением. Не следует и подсказывать, к какому разделу школьного курса математики относится предложенная задача, какие известные учащимся свойства и теоремы нужно применить при решении.

Решение нестандартной задачи — очень сложный процесс, для успешного осуществления которого учащийся должен уметь думать, догадываться. Необходимо также хорошее знание фактического материала, владение общими подходами к решению задач, опыт в решении нестандартных задач.

В процессе решения каждой задачи и ученику, решающему задачу, и учителю, обучающему решению задач, целесообразно четко разделять четыре ступени: 1) изучение условия задачи; 2) поиск плана решения и его составление; 3) осуществление плана, то есть оформление найденного решения; 4) изучение полученного решения — критический анализ результата решения и отбор полезной информации.

Даже при решении несложной задачи учащиеся много времени тратят на рассуждения о том, за что взяться, с чего начать. Чтобы помочь учащимся найти путь к решению задач, учитель должен уметь поставить себя на место решающего задачу, попытаться увидеть и понять источник его возможных затруднений, направить его усилия в наиболее естественное русло. Умелая помощь ученику, оставляющая ему разумную долю самостоятельной работы, позволит учащемуся развить математические способности, накопить опыт, который в дальнейшем поможет находить путь к решению новых задач.

“Лучшее, что может сделать учитель для учащегося, состоит в том, чтобы путем неназойливой помощи подсказать ему блестящую идею… Хорошие идеи имеют своим источником прошлый опыт и ранее приобретенные знания… Часто оказывается уместным начать работу с вопроса: “Известна ли вам какая-нибудь родственная задача?” (Пойа Д.). Таким образом, хорошим средством обучения решению задач, средством для нахождения плана решения являются вспомогательные задачи. Умение подбирать вспомогательные задачи свидетельствует о том, что учащийся уже владеет определенным запасом различных приемов решения задач. Если этот запас не велик (что вполне очевидно для учащихся VII—VIII классов), то учитель, видя затруднения учащегося, должен сам предложить вспомогательные задачи. Умело поставленные вспомогательные вопросы, вспомогательная задача или система вспомогательных задач помогут понять идею решения. Необходимо стремиться к тому, чтобы учащийся испытал радость от решения трудной для него задачи, полученного с помощью вспомогательных задач или наводящих вопросов, предложенных учителем.

Так, когда учащиеся затруднялись решить с помощью составления уравнения задачу “К некоторому двузначному числу слева и справа приписали по единице. В результате получили число в 23 раза большее первоначального. Найдите это двузначное число” ((5), № 1254), то в качестве вспомогательных задач мы предлагали следующие:

1. К числу х приписали справа цифру 4. Представьте полученное число в виде суммы, если х: а) двузначное число; б) трехзначное число.
2. К числу у приписали слева цифру 5. Представьте полученное число в виде суммы, если у: а) двузначное число; б) трехзначное число.

Конечно, думающий ученик задастся вопросом: как самому, без помощи учителя, находить вспомогательные задачи?

Безусловно, учащихся следует приучать самим составлять вспомогательные задачи, или упрощать условия предложенных задач так, чтобы без помощи учителя найти способы их решения.

Умение находить вспомогательные задачи, как и вообще умение решать задачи, приобретается практикой. Предлагая учащимся задачу, следует посоветовать выяснить, нельзя ли найти связь между данной задачей и какой-нибудь задачей с известным решением или с задачей, решающейся проще.

Для приобретения навыков решения довольно сложных задач нужно приучать школьников больше внимания уделять изучению полученного решения. Для этого мы предлагали учащимся видоизменять условия задачи, чтобы закрепить способ ее решения, придумывать задачи аналогичные решенным, более или менее трудные, с использованием найденного при решении основной задачи способа решения.

Решив задачу “В двух бочках было воды поровну. Количество воды в первой бочке сначала уменьшилось на 10%, а затем увеличилось на 10%. Количество воды во второй бочке сначала увеличилось на 10%, а затем уменьшилось на 10%. В какой бочке стало больше воды?” ((5), №1245), мы посчитали нужным задать учащимся вопросы: если вместо 10% взять 20%, 30%, а%? Какой вывод можно сделать?

Систематическая работа по изучению способов решения задач помогает учащимся не только научиться решать задачи, но и самим их составлять.

Так, после решения задачи “Докажите, что уравнение х2 – у2 = 30 не имеет решений в целых числах” ((5), № 1272), можно предложить учащимся попытаться сформулировать рассмотренную задачу в общем виде. Это будет выглядеть так: “Докажите, что уравнение х2 ‑ у2 = 4р + 2 (р — простое число) не имеет решения в целых числах”.

Конструирование задач — интересное занятие, один из верных способов решать задачи.

Умение учащихся составлять нестандартные задачи, решаемые нестандартными способами, свидетельствует о культуре их мышления, хорошо развитых математических способностях.

При анализе решения задачи полезно сопоставить решение данной задачи с ранее решенными, установить возможность ее обобщения.

Мы думаем, учитель должен постоянно помнить, что решение задач является не самоцелью, а средством обучения. Обсуждение найденного решения, поиск других способов решения, закрепление в памяти тех приемов, которые были использованы, выявление условий возможности применения этих приемов, обобщение данной задачи — все это дает возможность школьникам учиться на задаче.

Именно через задачи учащиеся могут узнать и глубоко усвоить новые математические факты, овладеть новыми математическими методами, накопить определенный опыт, сформировать умения самостоятельно, и творчески применять полученные знания.

Общеизвестна роль, которая отводится индукции и наблюдениям при обучении математике учащихся младших классов. Позднее индуктивный метод уступает место дедуктивному. При этом часто индуктивный способ решения задачи не проводится, решение выполняется дедуктивным способом. В результате от учащихся ускользают пути поиска решения задачи, что отрицательно сказывается на математическом развитии.

К сожалению, как свидетельствуют данные нашего исследования, при обучении учащихся математике (в частности, при обучении учащихся способам решения нестандартных задач) наблюдение и индукция (в том числе и полная) не заняли еще должного места. А между тем учитель должен знать, и по возможности довести до сознания учащихся тот факт, что математика является экспериментальной, индуктивной наукой, что наблюдение и индукция играли и играют большую роль при открытии многих математических фактов. Еще Л. Эйлер писал, что свойства чисел, известные сегодня, по большей части были открыты путем наблюдения и открыты задолго до того, как их истинность была подтверждена строгими доказательствами.

Поэтому уже в младших классах школы при обучении математике (да и другим предметам) надо учить школьников наблюдениям, прививать им навыки исследовательской творческой работы, которые могут пригодиться в дальнейшем, какой бы вид деятельности они не избрали после окончания школы.

Этой цели может служить, например, такое задание: “Число 6 представим в виде суммы всех его делителей, исключая из их состава само это число (6 = 1 + 2 + 3). Установите, сколько в первых двух десятках натуральных чисел (1, 2, 3, …, 20) существует чисел, равных сумме всех своих делителей (такие числа называют совершенными)”. Учащиеся путем перебора получают ответ. При этом следует добиваться от них понимания того, что полученный вывод (в первых двух десятках натуральных чисел содержится одно “совершенное” число — число 6, ближайшим следующим “совершенным” числом, которое можно обнаружить путем проб, является 28: 28 = 1 + 2 + 4 + 7 + 14) является строго (научно) обоснованным, так как примененный метод полной индукции (так называемый метод перебора) является научным и широко применяется в математике при доказательстве теорем и решении задач.

Методом полной индукции (рассмотрением всех возможных случаев) может быть уже в младших классах школы доказана теорема: “В первой сотне натуральных чисел содержится 25 простых чисел”.

Подчеркивая роль дедуктивных доказательств (дока­зательств в общем виде), учитель должен обратить внимание учащихся на роль наблюдений и неполной индукции при “открытии” математических закономерностей, при нахождении способа решения самых разнообразных математических задач, на роль полной индукции при обосновании найденных индуктивным путем закономерностей.

Поясним сказанное примерами. Рассмотрим задачу:

“Может ли: а) сумма пяти последовательных натуральных чисел быть простым числом; б) сумма квадратов пяти последовательных натуральных чисел быть простым числом?”

Прежде, чем решать эту задачу в общем виде, целесообразно на нескольких частных примерах выяснить, каким числом (простым или составным) могут быть указанные в задаче суммы. С помощью примеров можно получить гипотезы: а) сумма пяти последовательных натуральных чисел — число составное; б) сумма квадратов пяти последовательных натуральных чисел — число составное.

Полученные на примерах (с помощью неполной индукции) гипотезы легко доказываются в общем виде.

Другая задача: “Может ли разность двух трехзначных чисел, из которых второе записано теми же цифрами, что и первое, но в обратном порядке, быть квадратом натурального числа?”

На наших занятиях прежде чем решать эту задачу в общем виде, учащийся должен был на частных примерах, с помощью неполной индукции, получить предполагаемый ответ (выска­зать гипотезу): рассматриваемая разность не может быть равна квадрату какого-либо натурального числа. Дедуктивное обоснование этой гипотезы, как правило, не вызывает у учащихся затруднений.

Учащиеся должны понимать, что на частных примерах никакого утверждения доказать нельзя. Частный пример ничего не доказывает в математике, но он может подвести к правильному выводу.

В отличии от неполной индукции полная индукция имеет доказательную силу, и ее роль при решении многих алгебраических задач (прежде всего на делимость), трудно переоценить.

Приведем примеры. Пусть учащимся предложена задача: “Докажите, что любую сумму большую 7 к., можно уплатить трех- и пятикопеечными монетами не получая сдачи”.

Для решения этой задачи достаточно проверить, что трех- и пятикопеечными монетами можно уплатить 8, 9 и 10 к. (8 = 3 + 5, 9 = 3 + 3 + 3, 10 = 5 + 5), а затем добавлять монеты по 3 к.

Решив таким образом задачу, следует добиться от учащихся ясного понимания того, что задача решена с помощью полной индукции: все числа большие 7, разбили на три непересекающихся класса — 8 + 3k, 9 + 3k, 10 + 3k, где k ∈N, в каждом из которых решение задачи существует.

Можно оформить решение задачи несколько иначе, представив любое натуральное число п, большее 7, в одном из следующих видов:

п = 3k, где k ∈N, k ≥ 3;

п = 3k + 1, где k ∈N, k ≥ 3;

п = 3k + 2, где k ∈N, k ≥ 2.

Доказав в каждом из трех случаев возможность представления числа п требуемым образом, решим задачу методом полной индукции.

Для закрепления способа решения задач методом полной индукции полезно рассматриваемую задачу решить другим способом, разбив натуральные числа не на 3, а на 5 классов.

Учащиеся должны понимать, что метод полной индукции является научно-обоснованным методом и им можно пользоваться наряду с другими.

Ясно, что применять метод полной индукции можно лишь тогда, когда число рассматриваемых в задаче случаев конечно и не слишком далеко. Но иногда этим методом задачу можно решить много проще, чем другим.

Огромная значимость нахождения школьниками различных способов решения задач по математике не раз отмечалась на страницах методической литературы. Однако наши наблюдения показывают, что на уроках, как правило, рассматривается лишь один из способов решения задачи, причем не всегда наиболее рациональный. Приводимая в таких случаях аргументация в виде отсутствия достаточного количества времени на решение одной задачи различными способами не имеет под собой основы: для математического развития учащихся, для развития их творческого мышления гораздо полезнее одну задачу решить несколькими способами (если это возможно) и не жалеть на это времени, чем несколько однотипных задач одним способом. Из различных способов решения одной и той же задачи надо предложить учащимся выбрать наиболее рациональный, красивый.

При отыскании различных способов решения задач у школьников формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки. После нахождения очередного метода решения задачи учащийся, как правило, получает большое моральное удовлетворение. Учителю, как нам кажется, важно поощрять поиск различных способов решения задач, а не стремиться навязывать свое решение. Общие методы решения задач должны стать прочным достоянием учащихся, но наряду с этим необходимо воспитывать у них умение использовать индивидуальные особенности каждой задачи, позволяющие решить ее проще. Именно отход от шаблона, конкретный анализ условий задачи являются залогом успешного ее решения.

Особое внимание, на наш взгляд, следует обратить на решение задач арифметическим способом, так как именно решение задач арифметическим способом способствует развитию оригинальности мышления, изобретательности.

Часто учащиеся, ознакомившись со способом решения задач с помощью уравнения, не обременяют себя глубоким анализом условия задачи, стараются побыстрее составить уравнение и перейти к его решению. При этом и введение обозначений, и схема решений, как правило, соответствуют определенному шаблону.

В этом случае задача учителя — показать учащимся на примерах, что решение задач по шаблону часто приводит к значительному увеличению объема работы, а иногда и к усложнению решения, в результате чего увеличивается возможность появления ошибок. Поэтому учащимся полезно предложить, прежде чем составлять уравнение для решения задачи, внимательно изучить условие задачи, подумать над тем, какой способ решения наиболее соответствует ее условию, попытаться решить задачу без использования уравнений, арифметическим способом.

К сожалению, довольно широко распространено мнение, что решение задач повышенной трудности арифметическими методами излишне ввиду существования более сильного метода решения задач с помощью составления уравнения.

Существует и другое мнение, опирающееся на наблюдения за учащимися, согласно которому решение задач только алгебраическим методом ведет к одностороннему математическому развитию учащихся. Следует учитывать и то, что для составления уравнения следует использовать определенные арифметические навыки, понимание зависимостей между величинами. Кроме того, существует ряд задач, решение которых арифметическими методами изящнее и проще, чем с помощью уравнений.

В качестве примера рассмотрим задачу: “Два мотоциклиста выехали одновременно из пунктов А и В навстречу друг другу и встретились в 50 км от В. Прибыв в пункты А и В, мотоциклисты сразу же повернули назад и встретились вновь в 25 км от А. Сколько километров между А и В?”

Решение этой задачи с помощью уравнения представляет для учащихся определенные трудности: не случайно в школьном учебнике аналогичная задача помещена в разделе “Задачи повышенной трудности для 8 класса”.

На наших занятиях учащиеся решали эту задачу, не составляя уравнения, а рассуждая так. От начала движения до первой встречи оба мотоциклиста проехали расстояние равное АВ, а к моменту второй встречи проехали втрое большее расстояние. Таким образом, каждый из них до второй встречи проехал втрое больше, чем до первой. Мотоциклист, выехавший из пункта В, до первой встречи проехал 50 км. Следовательно, до второй встречи он проехал 150 км (50 × 3 = 150). Поэтому расстояние от А до В равно 125 км (150 – 25 = 125).

При таком подходе эту задачу могут решить учащиеся не только VIII, но и V класса.

Арифметический способ решения задач, когда шаблонный метод не легко приводит к результату, является, как свидетельствуют наши наблюдения, одним из лучших средств развития самостоятельного, творческого решения учащихся. С помощью специально подобранных задач, которые могут заинтересовать учащихся своей кажущейся простотой и тем, что их решение не сразу дается в руки, можно показать учащимся красоту, простоту и изящество логического рассуждения, приводящего к решению задачи. Иллюстрацией сказанного служит задача № 1287 из (5). (Всадник и пешеход одновременно отправились из пункта А в пункт В. Всадник, прибыв в пункт В на 50 мин. раньше пешехода, возвратился обратно в А. На обратном пути он встретился с пешеходом в двух километрах от В. На весь путь всадник затратил 1 час 40 минут. Найдите расстояние от А до В и скорость всадника и пешехода.)

Рассматривая решение задач несколькими способами, учитель на уроке и во внеклассной работе должен ориентировать учащихся на поиски красивых, изящных решений. Тем самым учитель будет способствовать эстетическому воспитанию учащихся и повышению их математической культуры.

Решая с учащимися ту или иную задачу, учитель должен стремиться к достижению двух целей. Первая — помочь ученику решить именно данную задачу, научить его решать задачи, аналогичные рассматриваемой; вторая — так развить способности ученика, чтобы он мог в будущем решить любую задачу школьного курса самостоятельно. Эти две цели, безусловно, связаны между собой, так как, справившись с заданной достаточно трудной для него задачей, учащийся несколько развивает свои способности к решению задач вообще.

Поэтому, преследуя вторую цель, при решении задач несколькими способами мы обращали внимание учащихся не только на наиболее рациональный, красивый способ решения данной задачи, но и на те способы, которые широко применяются при решении других задач и в некоторых случаях оказываются единственными. Поясним сказанное примером.

При решении задачи “Что больше: 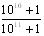или 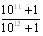?” ((5), № 1263) учащиеся, как правило, применяют наиболее естественный в данном случае способ решения — приведение дробей к общему знаменателю и сравнение их числителей.

Мы познакомили учащихся и с другими способами решения этой задачи, которые могли оказаться полезными при решении других задач.

Так, вычтя из обеих дробей по 0,1, мы получили дроби с одинаковыми числителями, которые сравним устно:

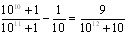
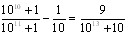
Так как 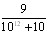> 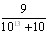, то > .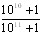

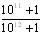Можно сравнить данные дроби и другим способом: умножив каждую из дробей на 10 и выделив единицу, будем иметь

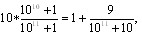
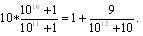
Так как > , то первая из данных дробей больше второй.

Иногда бывает целесообразным решить задачу в общем виде, хотя, как правило, числовые данные призваны упрощать решение задачи.

Семиклассникам была предложена задача: “Докажи­те, что не существует целых коэффициентов a, b, c, d, таких, что значение многочлена ax3 + bx2 + cx + d равно 1 при х = 19 и равно 2 при х = 62” ((5), № 1273).

Наряду с решением этой задачи с помощью составления системы уравнений для заданных числовых значений было дано решение задачи в общем виде. Из системы

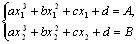
получали , откуда следовало, что для целых a, b, c, х1, х2, А, В выражение А – В всегда кратно х1 – х2. Подставив х1 = 62, х2 = 19, А = 2, В =1, получали, что А – В не делится на х1 – х2 (1 не делится на 43). Следовательно, утверждение задачи доказано.

Такой способ решения позволил нам (и ученикам) варьировать условие этой задачи, импровизировать на ее тему.

Например, было предложено учащимся заполнить недостающие данные в условиях следующих задач:

1. Докажи­те, что не существует целых коэффициентов a, b, c и d, таких, что значение многочлена ax3 + bx2 + cx + d равно 1 при х =… и равно 2 при х =… .
2. Докажи­те, что не существует целых коэффициентов a, b, c и d, таких, что значение многочлена ax3 + bx2 + cx + d равно … при х = 19 и равно … при х = 2.

Полезно также предложить учащимся составить и решить другие задачи на данную тему, основываясь на решении задачи в общем виде.

Заметим, что частое использование одного и того же метода при решении задач иногда приводит к привычке, которая становиться вредной. У решающего задачу вырабатывается склонность к так называемой психологической инерции. Поэтому, как бы ни казался учащимся простым найденный способ решения задачи, всегда полезно попытаться найти другой способ решения, который обогатит опыт решающего задачу. Кроме того, в некоторых случаях, получение того же результата другим способом служит лучшей проверкой правильности результата.

В заключение нами было проведено вторичное тестирование. Для проведения повторных испытаний использовался вариант методики альтернативный «рычаговому», предполагающий «открытие» условия равновесия ворота.

Результаты вторичного испытания отражены в таблице:

Как видим, результаты во всех классах улучшились. Однако, далеко не пропорционально. Сравнительно небольшое улучшение показателей «контрольного» класса мы склонны отнести за счет привыкания учащихся к подобному тестированию (и, конечно, мы полагаем, что изучение математики и по стандартной методике способствует активизации творческой мыслительной деятельности учащихся). Улучшение же показателей «экспериментальных» классов (причем в более значительной степени нежели в «контрольном» классе) дает нам основание считать гипотезу, выдвинутую нами в начале нашей работы, подтвердившейся и конкретные методические приемы по развитию продуктивного мышления школьников заслуживающими внимания.

Мы не считали наш результат конечным. Необходимо и далее разрабатывать и усовершенствовать приемы и методы развития продуктивного мышления, в зависимости от индивидуальных свойств и особенностей каждого отдельно взятого учащегося. Многое также будет зависеть от педагога-предметника, от того, будет ли он учитывать особенности познавательных процессов школьников и применять приемы активизации продуктивного мышления в ходе объяснения и закрепления материала, будет ли он строить свои уроки на ярком, эмоционально окрашенном рассказе или чтении текста учебника и от многих других фактов.

Анализируя проделанную работу можно сделать ряд выводов:

1. Экспериментальные занятия по курсу математики в 7 классах СШ № 18 г. Астрахани были достаточно продуктивны. Нам удалось достичь основной цели данного исследования — выработать ряд методических приемов, включенных в обычные программные уроки и позволяющих овладевать приемами продуктивного мышления, а следовательно облегчать усваиваемость материала и активизировать творческие способности школьников.
2. Анализ учебного материала, предшествующий практической части работы, позволил структурировать отобранный материал наиболее логичным и приемлемым способом, в соответствии с целями исследования.
3. Результатом проведенной работы являются несколько методических рекомендаций к курсу математики:

1. В целях совершенствования преподавания математики целесообразна дальнейшая разработка новых методик использования нестандартных задач.
2. Систематически использовать на уроках задачи, способствующие формированию у учащихся познавательного интереса и самостоятельности.
3. Осуществляя целенаправленное обучение школьников решению задач, с помощью специально подобранных упражнений, учить их наблюдать, пользоваться аналогией, индукцией, сравнениями и делать соответствующие выводы.
4. Целесообразно использование на уроках задач на сообразительность, задач-шуток, математических ребусов, софизмов.
5. Учитывать индивидуальные особенности школьника, дифференциацию познавательных процессов у каждого из них, используя задания различного типа.

Таким образом, проведенное нами исследование позволяет утверждать, что работа над формированием навыков продуктивного мышления у учащихся дело важное и необходимое. Поиск новых путей активизации творческой деятельности школьников является одной из неотложных задач современной психологии и педагогики.

1. Алгебра: Пробный учебник для 6 класса средней школы. Ш. А. Алимов, Ю. М. Калягин, Ю. В. Сидоров, М. И. Шабурин. М., 1988.
2. Алгебра: Пробный учебник для 7 класса средней школы. Ш. А. Алимов, Ю. М. Калягин, Ю. В. Сидоров, М. И. Шабурин. М., 1988.
3. Алгебра: Учебник для 6 класса средней школы. Ю. Н. Макарычев, Н. Г. Миндюк, К. С. Муравин и др.; Под ред. С. А. Теляковского. М., 1987.
4. Алгебра: Учебник для 7 класса средней школы. Ю. Н. Макарычев, Н. Г. Миндюк, К. С. Муравин и др.; Под ред. С. А. Теляковского. М., 1987.
5. Алгебра: Учебник для 7 класса средней школы. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Немков, С. Б. Суворова.; Под ред. С. А. Теляковского. М., 1991.
6. Атахов Р. Соотношение общих закономерностей мышления и математического мышления. Вопросы психологии, №5, 1995.
7. Василевский А. Б. Обучение решению задач по математике. Минск, 1988.
8. Вертгеймер М. Продуктивное мышление. М., 1987.
9. Давыдов В. В. Проблемы развивающего обучения: Опыт теоретического и экспериментального психологического исследования. М., 1986.
10. Калмыкова З. И. Продуктивное мышление как основа обучаемости. М., 1981.
11. Колягин Ю. М., Оганесян В. А. Учись решать задачи.
12. Кострикина Н. П. Задачи повышенной трудности в курсе алгебры 7-9 классов. М., 1991.
13. Крутецкий В. А. Основы педагогической психологии. М., 1972.
14. Крутецкий В. А. Психология математических способностей школьников. М., 1968.
15. Крутецкий В. А. Психология обучения и воспитания школьников.
16. Людмилов Д. С. Некоторые вопросы проблемного обучения математике. Пермь, 1975.
17. Матюшкин А. М. Проблемные ситуации в мышлении и обучении. М., 1972.
18. Особенности обучения и психического развития школьников 13-17 лет. Под ред. И. В. Дубровиной, Б. С. Кругловой. М., 1988.
19. Пичурин Л. Ф. За страницами учебника алгебры. М., 1990.
20. Пойа Д. Как решить задачу: Пособие для учителей. М., 1961.
21. Пойа Д. Математика и правдоподобные рассуждения. М., 1970.
22. Пойа Д. Математическое открытие. М., 1976.
23. Пономарев Я. А. Знание, мышление и умственное развитие. М., 1967.
24. Пономарев Я. А. Психология творческого мышления. М., 1960.
25. Пономарев Я. А. Психология творчества и педагогика. М., 1976.
26. Проблемы диагностики умственного развития учащихся. Под ред. Н. А. Менчинской. М., 1961.
27. Рубинштейн С. Л. О мышлении и путях его исследования. М., 1958.
28. Семенов Е. М., Горбунова Е. Д. Развитие мышления на уроках математики. Свердловск, 1966.
29. Фридман Л. М. Психолого-педагогические основы обучения математике в школе. М., 1983.
30. Фридман Л. М., Турецкий Е. Н. Как научиться решать задачи. М., 1989.
31. Якиманская И. С. Развивающее обучение. М., 1979.
32. Яковлева Е. Л. Психологические условия развития творческого потенциала у детей школьного возраста. Вопросы психологии, №5, 1994.

Работа Гудырина С. Н. исследует формы учебной деятельности на уроках математики. Она освещает вопрос целенаправленного развития навыков продуктивного мышления школьников.

Структура и содержание дипломной работы отвечает поставленным целям.

Первая часть выполнена в теоретическом плане. В ней интересно и глубоко рассмотрены вопросы теории продуктивного мышления. Анализ большого количества литературы по данной тематике позволил автору определить понятие “продуктивное мышление”, основные его показатели и выделить некоторые психолого-педагогические принципы развития продуктивного мышления учащихся.

Практическая часть проведена в форме исследования и представляет собой поиск наиболее эффективных форм учебной деятельности, позволяющих строить учебный процесс на уроках математики с учетом творческих способностей школьников.

Выводы и оценки автора аргументированы, подтверждены фактическим материалом, полученным в ходе проведенного эксперимента.

Необходимо отметить самостоятельность и творческий подход автора в постановке цели и выдвижении гипотезы, подборе экспериментальных методик.

Мы полагаем, что работа Гудырина С. Н. отвечает всем требованиям дипломной работы, она, несомненно, будет способствовать дальнейшей разработке указанной проблематики.

Работа заслуживает высокой оценки “отлично”.

Кандидат психологическихнаук, доцент, заведующий кафедрой психологии Кайгородов Б. В.

Старший преподаватель кафедры математическогоанализа Сикорская Л. В.