Пирамиды

МОУ «Средняя образовательная школа села Чёрный Яр»

Реферат

«Пирамиды»

Выполнила:

Черёмина А.

ученица 11 А кл.

Руководитель:

Халяпина Л.А.

2005 г.

Содержание

Введение

Значимость пирамиды в моем познании

Основная часть:

1. Исторические сведения о пирамиде

2. Различные трактовки определения пирамиды

3. Основные элементы

4. Сечения пирамиды

5. Виды пирамид

  • правильная пирамида
  • усеченная пирамида

6. Площадь пирамиды

7. Измерение объема

8. Тетраэдр – простейшая пирамида

  • основные элементы
  • виды тетраэдров
  • свойства тетраэдра

9. Задачи

10. Решение задач

Заключение

Список использованной литературы

Введение

Египетские пирамиды – одно из семи чудес света.… Как загадочны эти фигуры! Сколько тайн хранят они в себе! С самого детства я задумывалась об этом. Они манили меня к себе своей таинственностью. Когда я пошла в десятый класс, мы начали изучать стереометрические фигуры и, конечно, затронули тему «Пирамида». Мне стало очень интересно, и я решила изучить свойства этой необычной фигуры немного подробнее, ведь тема «Пирамиды» затрагивает глубокие аспекты современных научных дисциплин и является одной из наиболее актуальных для пытливых умов современных ученых. Пирамиды представляют интерес для математиков, историков, физиков, биологов, медиков, философов. Чем больше мы узнаем о пирамидах, тем больше у нас возникает вопросов. Хотя не стоит забывать и о том, что пирамиды таят в себе ответы на огромное количество вопросов, которыми сейчас задается наука.

Пирамиды, несмотря на свою древность, могут многому нас научить. Исследованием пирамид с использованием новейших приборов занимались американцы, японцы. Пирамиды снимали со спутников. Американская станция "Маринер"' передала фотографии с Марса, на которых изображены такие же пирамиды, что наводит на мысль об их внеземном происхождении. Так что же такое пирамиды?

Исторические сведения о пирамиде

Усыпальницы египетских фараонов. Крупнейшие из них — пирамиды Хеопса, Хефрена и Микерина в Эль-Гизе в древности считались одним из Семи чудес света. Возведение пирамиды, в котором уже греки и римляне видели памятник невиданной гордыни царей и жестокости, обрекшей весь народ Египта на бессмысленное строительство, было важнейшим культовым деянием и должно было выражать, по всей видимости, мистическое тождество страны и ее правителя. Население страны работало на строительстве гробницы в свободную от сельскохозяйственных работ часть года. Ряд текстов свидетельствует о том внимании и заботе, которые сами цари (правда, более позднего времени) уделяли возведению своей гробницы и ее строителям. Известно также об особых культовых почестях, которые оказывались самой пирамиде.

Пирамиды выстроены на левом — западном берегу Нила (Запад — царство мертвых) и возвышались над всем городом мертвых — бесчисленными гробницами, пирамидами, храмами.

Самая большая из трех — пирамида Хеопса (зодчий Хемиун, 27 в. до н. э.). Ее высота была изначально 147 м, а длина стороны основания — 232 м. Для ее сооружения потребовалось 2 млн. 300 тыс. огромных каменных блоков, средний вес которых 2,5 т. Плиты не скреплялись строительным раствором, лишь чрезвычайно точная подгонка удерживает их. В древности пирамиды были облицованы отполированными плитами белого известняка, вершины их были покрыты медными листами, сверкавшими на солнце (известняковую обшивку сохранила только пирамида Хеопса, покрытие других пирамид арабы использовали при строительстве Белой мечети в Каире).

Близ пирамиды Хефрена возвышается одна из крупнейших статуй древности и нашего времени — высеченная из скалы фигура лежащего сфинкса с портретными чертами самого фараона Хефрена.

Великие пирамиды были окружены рядом небольших усыпальниц жен фараонов и их приближенных. В такие комплексы обязательно входили святилища Верхнего и Нижнего Египта, большие дворы для проведения праздника хеб-су, заупокойные храмы, служители которых должны были поддерживать культ умершего царя. Пространство вокруг пирамиды, окруженное стенами, посредством длинного крытого перехода соединялось с храмом на берегу Нила, где встречали тело фараона и начинались погребальные церемонии.

Все пирамиды точно сориентированы по сторонам света, что свидетельствует о высоком уровне астрономических знаний древних египтян, расчет углов наклона граней совершенно безукоризнен. В пирамиде Хеопса угол наклона таков, что высота пирамиды равна радиусу воображаемой окружности, в которую вписано основание пирамиды.

Замечательной инженерной находкой древних зодчих и строителей было сооружение в толще каменной кладки над погребальной камерой пяти разгрузочных камер, с помощью которых удалось снять и равномерно распределить колоссальную нагрузку на ее перекрытия. Помимо камер в пирамиде есть и другие пустоты — коридоры, проходы и галереи, входы в которые были тщательно замурованы и замаскированы. Тем не менее захоронения в пирамидах были разграблены, видимо, довольно скоро после погребения фараонов. Воры хорошо знали все ловушки, так что они, скорее всего, были связаны либо со строителями, либо со жрецами, осуществлявшими захоронения.

Сооружения в Эль-Гизе своей грандиозностью и видимой бесполезностью поражали воображение уже в древности, что лучше всего передает арабская пословица: «Все на свете боится времени, но время боится пирамид».

Различные трактовки определения пирамиды

Пирамиду Евклид определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости (основания) сходятся в одной точке (вершине). Это определение подвергалось критике уже в древности, например, Героном, предложившим следующее определение пирамиды: это фигура, ограниченная треугольниками, сходящимися в одной точке, и основанием которой служит многоугольник. Важнейшим недостатком этого определения является использование неопределенного понятия основания. Тейлор определил пирамиду как многогранник, у которого все грани, кроме одной, сходятся в одной точке. Лежандр в “Элементах геометрии” так определяет пирамиду: “Телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”. После этой формулировки разъясняется понятие основания. Определение Лежандра является явно избыточным, т.е. содержит признаки, которые можно вывести из других. А вот еще одно определение, которое фигурировало в учебниках XIX века: пирамида - телесный угол, пересеченный плоскостью.

Чаще всего учащиеся сталкиваются со следующим определением, которое я считаю самым объективным:

Пирамидой называется многогранник, который состоит из плоского многоугольника, – основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды.

Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

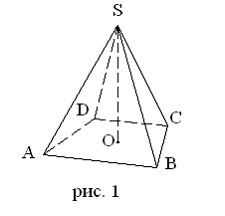
У пирамиды, изображенной на рис. 1, основание – многоугольник ABCD, вершина пирамиды – S, боковые ребра – SA, SB, SC, SD, боковые грани – ∆ASB, ∆BSC, ∆CSD, ∆ASD, высота SO.

Чтобы получить пирамиду, достаточно какой-нибудь многогранный угол S пересечь произвольной плоскостью ABCD и взять отсеченную часть SABCD (рис. 2).

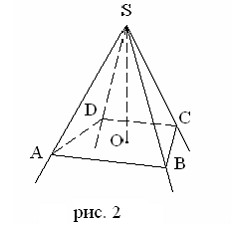
Диагональные сечения пирамиды

Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники (рис. 3). В частности, треугольниками являются диагональные сечения. Это сечение плоскостями, проходящими через два несоседних боковых ребра пирамиды.

Плоскость, проведенная через вершину пирамиды и через какую-нибудь диагональ основания, называется диагональной плоскостью (рис. 4).

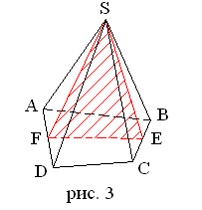∆CEF – сечение пирамиды SABCD

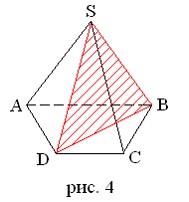∆SDB – диагональное сечение пирамиды SABCD

Сечение пирамиды плоскостью с заданным следом g на плоскости

1. Проведем прямую CD, CD×g ≡ F, F є (SCD)

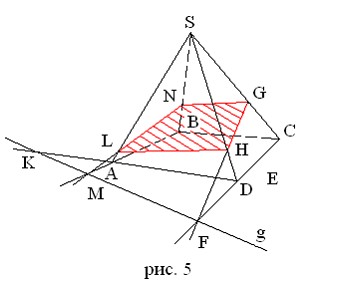
2. Рассмотрим грань SCD. Проведем прямую FE, получим точки пересечения с ребрами пирамиды: SD×FE ≡ H и SC×FH ≡ G

3. Проведем прямую AD. Найдем точку пересечения AD со следом g,

AD×g ≡ K

4. Теперь уже в грани SAD появились две точки K и H. Проведем прямую KH, она пересекает ребро SA в точке L: KH×SA ≡ L

5. Проведем прямую AB, найдем пересечение с прямой g:

g×AB ≡ M

6. В грани получились две точки M и L. Получаем прямую ML. Находим пересечение с ребром SB: CB×ML ≡ N

7. Соединим N и G. Сечение GHLN построено (рис. 5).

Правильная пирамида

Определение: Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания.

Очевидно, у правильной пирамиды боковые ребра равны; следовательно, боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

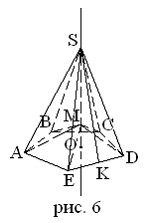
Пусть SABCDE – правильная пятиугольная пирамида (рис. 6). Тогда по определению ее основание ABCDE – правильный плоский пятиугольник; центр основания пирамиды O – основание высоты пирамиды SO.

Высота боковой грани правильной пирамиды, проведенная из вершины пирамиды, называется апофемой.

Например, SK – апофема правильной пирамиды.

При повороте вокруг прямой OS на 360˚/5 правильный многоугольник ABCDE каждый раз совместится с собой, тогда совместится с собой и пирамида. Значит, прямая, на которой лежит высота правильной n-угольной пирамиды, есть ее ось симметрии n-го порядка.

Отсюда следует, что у правильной пирамиды:

  1. боковые ребра равны
  2. боковые грани равны
  3. апофемы равны
  4. двугранные углы при основании равны
  5. двугранные углы при боковых ребрах равны
  6. каждая точка высоты равноудалена от всех вершин основания
  7. каждая точка высоты равноудалена от всех боковых граней

Теорема: Если в пирамиде все боковые ребра равны, то вершина проектируется в центр описанной около основания окружности.

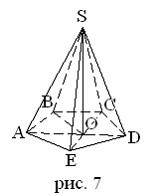
Дано: SABCDE – правильная пирамида (рис. 7); SA = SB = SC = SD = SE; SOABCDE

Доказать: O – Центр описанной окружности

Доказательство: S – точка, равноудаленная от всех вершин многоугольника ABCDE.

Т.к наклонные равны, значит и проекции будут равны → O – центр окружности, описанной около многоугольника.

Теорема: Если в пирамиде все двугранные углы при основании равны, то вершина проектируется в центр вписанной в основание окружности.

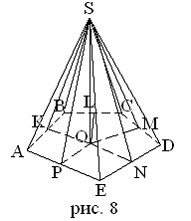
Дано: SABCDE – правильная пирамида (рис. 8); AB = BC = CD = DE = AE; SOABCDE

Доказать: O – центр вписанной окружности

Доказательство:

Проведем OKAB, OLBC, OMCD, ONED, OPAE, тогда по теореме о трех перпендикулярах SKAB, SLBC, SMCD, SNED, SPAE, значит, SKO, SLO, SMO, SNO, SPO – линейные углы двугранных углов при основании пирамиды. По условию двугранные углы равны, значит и соответствующие линейные углы будут равны. Поэтому ∆SKO = ∆SLO = ∆SMO = ∆SNO = ∆SPO как прямоугольные треугольники, в которых катет SO общий, а острые углы равны. Из равенства треугольников следует, что OK = OL = OM = ON = OP → точка O равноудалена от всех сторон многоугольника ABCDE. Значит, она – центр вписанной окружности.

Теорема доказана.

Симметрия правильной пирамиды

1. Плоскости симметрии: при четном числе сторон основания — плоскости, проходящие через противолежащие боковые ребра; и плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней (рис. 9).

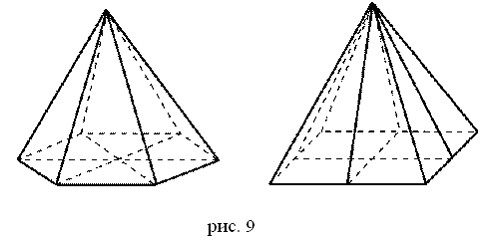
2. Ось симметрии: при четном числе сторон основания — ось симметрии, проходящая через вершину правильной пирамиды и центр основания (рис. 10).

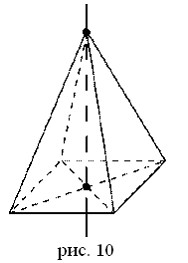
Усеченная пирамида

(*)Теорема:

Плоскость, пересекающая пирамиду и параллельная ее основанию отсекает подобную пирамиду.

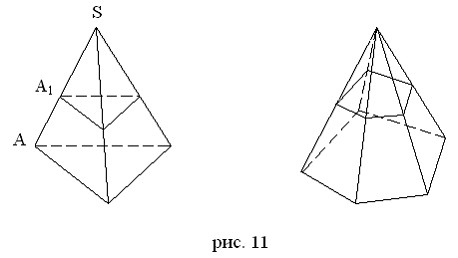
Доказательство:

Пусть S – вершина пирамиды, A – вершина основания и A1 – точка пересечения секущей плоскости с боковым ребром SA (рис. 11). Подвергнем пирамиду преобразованию гомотетии (фр. homothetie греч. homos равный, одинаковый, общий + thetos расположенный) относительно вершины S с коэффициентом гомотетии:

k = SA1/SA

При этой гомотетии плоскость основания переходит в параллельную плоскость, а следовательно, вся пирамида – в отсекаемую этой плоскостью часть. Так как гомотетия есть преобразование подобия, то отсекаемая часть пирамиды является пирамидой подобной данной. Теорема доказана.

По теореме (*) плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает от нее подобную пирамиду. Другая часть представляет собой многогранник, который называется усеченной пирамидой. Грани усеченной пирамиды, лежащие в параллельных плоскостях, называются основаниями; остальные грани называются боковыми гранями. Основания усеченной пирамиды подобные многоугольники, их стороны попарно параллельны, поэтому боковые грани – трапеции.

Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания на плоскость другого основания. Сечение плоскостью, проходящей через два боковых ребра усеченной пирамиды, не лежащих в одной грани, называется диагональным.

Например, многогранник ABCDA1B1C1D1 – усеченная пирамида (рис. 12). Плоский многоугольник ABCDE и сечение A1B1C1D1 – основания усеченной пирамиды. Трапеции A1E1EA, E1D1DE, C1D1DC, B1C1CB, A1B1BA – боковые грани. HH1 – высота. E1C1CE – диагональное сечение усеченной пирамиды.

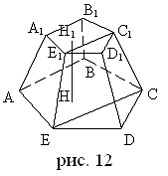
Теорема: Если пирамида пересечена плоскостью, параллельной основанию, то:

  1. боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части;
  2. Сечение – это многоугольник, подобный основанию;
  3. Площади сечения и основания относятся как квадраты их расстояний от вершины;

Следствие: Площадь сечения параллельного основанию пирамиды – квадратная функция расстояния его плоскости от вершины (или основания) пирамиды.

Чтобы построить усеченную пирамиду, сначала намечают карандашом полную пирамиду, проводят сечение, параллельное основанию, проводят ребра усеченной пирамиды, а верхнюю часть стирают.

Правильная усеченная пирамида

Усеченная пирамида называется правильной, если она составляет часть правильной пирамиды (рис. 13).

Высота боковой грани правильной усеченной пирамиды называется апофемой.

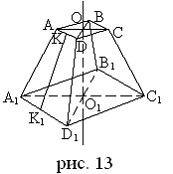
Например, KK1 – апофема правильной усеченной пирамиды. Прямая OO1 называется осью правильной усеченной пирамиды.

Площадь пирамиды

Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему.

Доказательство:

Если сторона основания а, число сторон n, то боковая поверхность пирамиды равна:

a∙l∙n/2 =a∙n∙l/2=pl/2

где l – апофема, а p – периметр основания пирамиды. Теорема доказана.

Эта формула читается так:

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему пирамиды.

Sбок = pl/2

Площадь полной поверхности пирамиды вычисляется по формуле:

Sполн = Sбок + Sосн

Если пирамида неправильная, то ее боковая поверхность будет равна сумме площадей ее боковых граней.

Площадь боковой и полной поверхности усеченной пирамиды

Теорема: Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Дано: n-угольная правильная усеченная пирамида, l – апофема, p и p1 – периметры оснований.

Доказать: Sбок = ½(p+p1) ∙l

Доказательство: В правильной усеченной пирамиде все боковые грани – равные между собой трапеции. Пусть основания трапеции a и a1, ее высота k, тогда Sгр. = ½(a + a1)∙l, таких граней n,

следовательно, Sбок = n ½ (a + a1) l = ½ (na + na1)∙l, т.е. Sбок = ½ (p+p1)∙l

Теорема доказана.

Измерение объема пирамиды

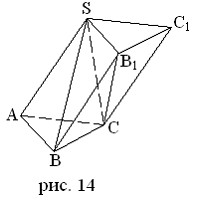
Пусть SABC – треугольная пирамида с вершиной S и основанием ABC. Дополним эту пирамиду до треугольной призмы с тем же основанием и высотой (рис. 14). Эта призма составлена из трех пирамид: данной пирамиды SABCD и еще двух треугольных пирамид SCC1B1 и SCBB1.

У второй и третьей пирамид равные основания – ∆CC1B1 и ∆B1BC и общая высота, проведенная из вершины S. Поэтому у них равные объемы.

У первой и третьей пирамид тоже равные основания – ∆SAB и ∆BB1C и совпадающие высоты, проведенные из вершины C. Поэтому у них тоже равные объемы.

Значит, все три пирамиды имеют один и тот же объем. Так как сумма этих объемов равна объему призмы, то объемы пирамид равны SH/3.

Итак, объем любой треугольной пирамиды равен одной трети произведения площади основания на высоту:

V = 1/3∙SH

Пусть теперь имеем любую, не обязательно треугольную пирамиду. Разобьем ее основание на треугольники ∆1, ∆2, …∆n . Пирамиды, у которых основаниями являются эти треугольники, а вершинами – вершина данной пирамиды, составляют данную пирамиду. Объем данной пирамиды равен сумме объемов составляющих ее пирамид. Т.к. все они имеют ту же высоту H, что и данная пирамида, то объем ее равен:

V = 1/3∙H ∙ (S1 + S2 + …Sn) = 1/3∙SH

Итак, объем любой пирамиды равен одной трети произведения площади ее основания на высоту.

V = 1/3∙SH

Объем усеченной пирамиды

Теорема: Объем усеченной пирамиды равен V = h/3∙(S+S1+√SS1)

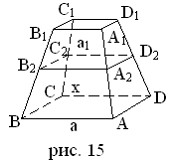
Дано: ABCDA1B1C1D1 – усеченная пирамида (рис. 15), S и S1 – площади оснований, h – высота.

Доказать: V = h/3∙(S+S1+√SS1)

Доказательство: В усеченной пирамиде площадь сечения плоскостью, параллельной основанию, есть квадратная функция от расстояния сечения до этого основания. Значит, применима формула Симпсона:

(1) V = h/6∙(Sн + 4Sc + Sв)

Sн = S, Sв = S1.Найдем Sc.

Пусть A2B2C2D2 – среднее сечение. Примем AB = a, A1B1 = a1, A2B2 = x. Основания и среднее сечение – подобные многоугольники, и потому

S : Sc : S1 = a2 : x2 : a12

отсюда

(2) a : x : a1 = √S : √Sc : √S1

AA1B1B – трапеция, x – ее средняя линия, значит,

(3) = (a + a1)/2

Из (2) следует, что a = m√S, x = m√Sc, a1 = m√S1, где m – общая мера. Подставим эти значения в (3):

m√Sc = (m√S + m√S1)/2, значит, √Sc = (√S + √S1)/2

Sc = (√S + √S1)2/4.

Подставим значения Sн, Sв и Sc в (1):

V = h/6∙(S + (√S + √S1)2 + S1) = h/6(S + S + 2√SS1 + S1 + S1), т.е.

V = h/3∙(S+S1+√SS1)

Тетраэдр

Изо всех рассмотренных пирамид наибольший интерес у меня проявляется к простейшей пирамиде, называемой тетраэдром. Я постараюсь более подробно рассмотреть тетраэдр и его свойства.

Слово «тетраэдр» образовано из двух греческих слов: tetra – «четыре» и hedra – «основание, грань». Тетраэдр ABCD задается четырьмя своими вершинами – точками A, B, C, D, не лежащими в одной плоскости: грани тетраэдра – четыре треугольника; ребер у тетраэдра шесть. В отличие от произвольной пирамиды (n – угольной пирамиды, n≥4) в качестве основания тетраэдра может быть выбрана любая его грань.

Как треугольник – простейший многоугольник, так тетраэдр, или треугольная пирамида – простейший многогранник. Геометрия тетраэдра ничуть не менее богата, чем геометрия его плоского собрата – треугольника, многие свойства которого в преображенном виде мы находим у тетраэдра. Немало общего имеет тетраэдр с четырехугольником – ведь у обоих по четыре вершины.

Треугольники принято классифицировать по степени их симметричности: правильные или равносторонние треугольники имеют три оси симметрии, равнобедренные – одну. Самый симметричный тетраэдр правильный, ограниченный четырьмя правильными треугольниками. Он имеет 6 плоскостей симметрии – они проходят через каждое ребро перпендикулярно противолежащему ребру и 3 оси симметрии, проходящие через середины противолежащих ребер. Менее симметричны правильные треугольные пирамиды (т.е. тетраэдры с равными гранями – 3 оси симметрии). Правильная пирамида переходит сама в себя при поворотах вокруг высоты на 120˚ и 240˚, а также при симметриях относительно плоскостей, проходящих через ось и боковые ребра. По сложившейся не очень логичной традиции, термин «правильный тетраэдр» обозначает частный случай правильной треугольной пирамиды – тетраэдр, у которого все ребра равны, т.е. все грани – равносторонние треугольники. Такой тетраэдр обладает наибольшим набором самосовмещений. Имеется 12 поворотов, переводящих его в себя, 6 симметрий относительно плоскостей и еще 6 движений, сочетающих поворот с симметрией.

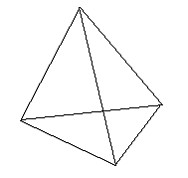
Правильный тетраэдр – не что иное, как «стереометрический близнец» самого симметричного треугольника – правильного.

Тетраэдр и сферы

Любой треугольник имеет единственную вписанную и описанную окружности. Точно также у любого тетраэдра есть единственная вписанная (касающаяся всех граней) и единственная описанная (проходящая через все вершины) сферы. Доказательства этих свойств повторяют соответствующие планиметрические: центр вписанной сферы равноудален от всех вершин и лежит на пересечении перпендикуляров, восстановленных к граням из центров их описанных окружностей (т.е. четыре перпендикуляра пересекаются в одной точке). Но кроме граней и вершин тетраэдр имеет еще и ребра. Возникает вопрос: можно ли провести сферу, касающуюся всех его шести ребер (ее называют полувписанной; рис. 16)?

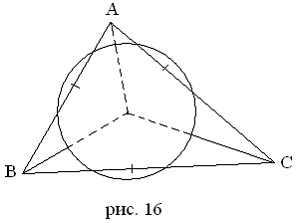
…Иногда. Здесь тетраэдр ведет себя, как четырехугольник, и условия существования полувписанной сферы повторяет признак описанного четырехугольника: такая сфера существует тогда и только тогда, когда суммы длин каждой пары противоположных ребер тетраэдра равны между собой:

AB + CD = AC + BD = AD + BC

Тетраэдры, имеющие полувписанную сферу, называются каркасными. По сути дела, это все тот же планиметрический признак, но примененный к пространственным четырехугольникам – в данном случае четырехугольникам, образованным двумя парами противоположных ребер тетраэдра. Но еще большие неожиданности обнаруживаются при исследовании вневписанных сфер тетраэдра, т.е. сфер, касающихся плоскостей всех четырех его граней, но лежащих вне тетраэдра. Как известно, у любого треугольника имеется три вневписанные окружности. Плоскости граней тетраэдра разбивают пространство на 15 областей (рис. 17). Кроме четырех трехгранных углов, примыкающих к вершинам, остальные 11 областей ограничены всеми четырьмя плоскостями. Внутри тетраэдра, а также внутри четырех «постаментов» – областей, примыкающих к граням, – сфера, касающаяся всех плоскостей, всегда есть. А вот с шестью областями, примыкающими к ребрам и по форме напоминающими четырехскатные крыши или чердаки, дело обстоит сложнее. Оказывается, из двух «чердаков» при противоположных ребрах только у одного может быть вписанная сфера. Таким образом, у правильного тетраэдра – а у него все «чердаки» одинаковы – «чердачных» сфер вообще нет, иначе они присутствовали бы во всех «чердаках». Итак, тетраэдр имеет не менее четырех и не более семи вневписанных сфер, причем все промежуточные случаи возможны.

Медианы тетраэдра

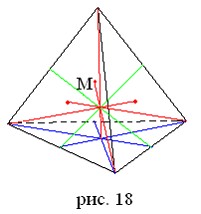
Для любого тетраэдра справедлив аналог теоремы о пересечении медиан треугольника в одной точке, в которой они делятся в отношении 2:1. Так, 6 плоскостей, проведенных через ребра тетраэдра и середины противолежащих ребер, пересекаются в одной точке – в центроиде тетраэдра.

Медианами в тетраэдре называются отрезки, соединяющие его вершины с центроидами противоположных граней. Эти четыре отрезка всегда пересекаются в одной точке M и делятся в ней в отношении 3:1, считая от вершин (рис. 18).

Через ту же точку проходят и бимедианы – отрезки, соединяющие середины противоположных ребер тетраэдра, причем они делятся точкой M пополам.

Центроид тетраэдра, как и центроид треугольника, является центром равных масс, помещенных в его вершины, – обстоятельство, которое можно использовать для доказательства приведенных выше свойств. Чисто геометрически их можно доказать с помощью следующей полезной конструкции.

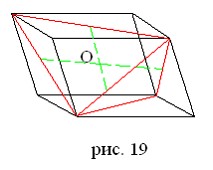
Проведем через каждое ребро тетраэдра плоскость, параллельную противоположному ребру (рис. 19). Получим три пары параллельных плоскостей, ограничивающих параллелепипед, называемый описанным параллелепипедом тетраэдра. Ребра тетраэдра являются диагоналями граней параллелепипеда, середины ребер – их центроидами. Отсюда следует, что все бимедианы проходят через центр O параллелепипеда и делятся им пополам. Нетрудно увидеть, что медианы тетраэдра лежат на диагоналях граней параллелепипеда и также проходят через точку O.

Ортоцентрический и прямоугольный тетраэдры

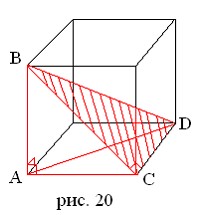
Медианы тетраэдра «ведут себя примерно» – как и в треугольнике, они всегда проходят через одну и ту же точку. Иначе обстоит дело с высотами – перпендикулярами, опущенными из вершин тетраэдра на противоположные грани. Высоты треугольника пересекаются в одной точке – ортоцентре. То же верно и для правильных тетраэдров, в частности для правильных треугольных пирамид. Но, например, у тетраэдра ABCD, вписанного в куб, как показано на рис. 20, ребра AB и DC сами являются высотами и не пересекаются.

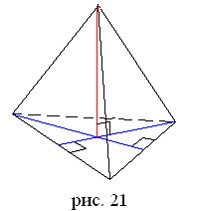
И все же ортоцентр существует у достаточно широкого класса тетраэдров. Они так и называются – ортоцентрические тетраэдры. Любой из них можно получить, взяв в качестве основания произвольный треугольник и соединив его вершины с любой точкой на перпендикуляре к его плоскости, восстановленном из его ортоцентра (рис. 21). И обратно, основания всех высот ортоцентрического тетраэдра – ортоцентры его граней. Приведем еще несколько критериев (т.е. необходимых и достаточных условий) ортоцентричности: тетраэдр является ортоцентрическим тогда и только тогда, когда его противоположные ребра перпендикулярны; или середины всех шести ребер лежат на одной сфере; или все ребра описанного параллелепипеда равны.

Некоторые свойства треугольника, связанные с ортоцентром, например теорема о прямой Эйлера и об окружности девяти точек в соответственно измененном виде, можно найти и у ортоцентрического тетраэдра.

Центроид ортоцентрического тетраэдра лежит на отрезке между ортоцентром H и центром описанной сферы O и делит этот отрезок пополам, а точка, которая разбивает отрезок OH в отношении 1:2 является центром «сферы 12 точек» – на ней лежат ортоцентры и центроиды всех граней, а также точки, делящие отрезки от H до вершин в отношении 1:2. Доказательства этих теорем не так уж и сложны, хотя и требуют пространственного воображения.

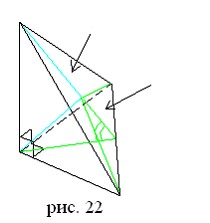
Об одном виде ортоцентрических тетраэдров стоит сказать отдельно – о тетраэдре, в вершине которого сходятся три взаимно перпендикулярных ребра (рис. 22). Очевидно, эта вершина M и будет его ортоцентром. Такой тетраэдр называется прямоугольным. Для него выполняется своего рода «теорема Пифагора»: если S1, S2, S3 – площади его прямоугольных граней («катетов»), а S – площадь четвертой грани («гипотенузы»), то:

S2= S12+ S22+ S32

В самом деле, проекции трех «катетов» на «гипотенузу» разбивают ее на три треугольника. Поскольку при проекции площадь фигуры умножается на косинус угла между ее плоскостью и плоскостью проекции, то:

(*) S=S1 ∙cos α1+S2∙ cos α2+S3 ∙cos α3

где α1 – угол между плоскостями «гипотенузы» и соответствующего «катета». В то же время каждый из «катетов» совпадает с проекцией «гипотенузы» на его плоскость, поэтому cos αi=Si/S. Остается подставить выражение косинусов через площади в уравнение (*).

Равногранный тетраэдр

Как мы определяем правильный, или равносторонний, треугольник? Естественно, как треугольник, все стороны которого равны. А что такое «стороны» тетраэдра? Если считать, что это ребра, то аналогичное стереометрическое определение приведет к понятию правильного тетраэдра? Но может быть «сторонами» тетраэдра следует считать его грани? Тогда мы приходим к следующему определению: тетраэдр, все грани которого равны (т.е. являются равными треугольниками), называется равногранным. На первый взгляд равногранный тетраэдр – это правильный тетраэдр, и никакой другой. В действительности гранью равногранного тетраэдра может быть любой остроугольный треугольник. Перечислим важнейшие свойства равногранных тетраэдров. Первые два свойства указывают и общий способ их построения:

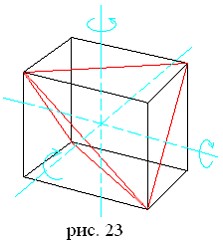
  1. описанный параллелепипед равногранного тетраэдра – прямоугольный (рис. 23);
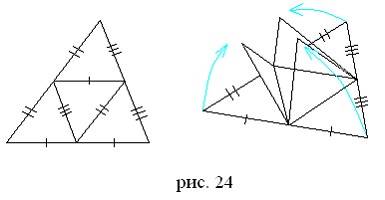
  2. развертка тетраэдра, полученная при разрезании его по трем сходящимся в одной вершине ребрам, – треугольник (рис. 24; этот треугольник должен быть остроугольным, потому что тупоугольный или прямоугольный при сгибании по соседним линиям не сложится в тетраэдр). Набор самосовмещений произвольного равногранного тетраэдра не так богат, как у правильного тетраэдра.
  3. у него имеется три оси симметрии (это общие перпендикуляры, проведенные к противоположным ребрам, они же бимедианы; рис. 23). Однако этих симметрий хватает, чтобы можно было совместить любые две указанные грани или вершины, но не ребра.

Пользуясь свойствами 1 – 3 и непосредственно определением, легко вывести, что у равногранного тетраэдра:

    1. все трехгранные углы равны;
    2. все медианы равны;
    3. все высоты равны;
    4. центры вписанной и описанной сфер и центроид совпадают;
    5. радиусы описанных окружностей граней равны;
    6. периметры граней равны;
    7. площади граней равны;

    Некоторые из этих свойств настолько очевидны, что на первый взгляд даже не заслуживают упоминания. Замечательно другое: все эти свойства равносильны друг другу и каждое из них в отдельности обеспечивает равногранность тетраэдра. Более всего впечатляет свойство 10: Для равенства граней тетраэдра достаточно, чтобы были равны между собой их площади!

    Итак, все десять перечисленных условий являются одновременно и свойствами и признаками равногранного тетраэдра. Чтобы вывести равногранность из какого-нибудь условия, надо выстроить целую цепочку промежуточных условий, в которой каждое последующее – прямое следствие предыдущего.

    Задачи

    1. Одно из самых грандиозных сооружений древности – пирамида Хеопса – имеет форму правильной четырехугольной пирамиды с высотой ≈ 150 м и боковым ребром ≈ 220 м. Найдите объем и площадь боковой поверхности этой пирамиды.

    2. Крыша имеет форму пирамиды с квадратным основанием 4,5 м × 4,5 м и углом наклона грани к основанию в 45˚. Сколько листов железа размером 70 см × 140 см нужно для покрытия крыши, если на отходы нужно добавить 10% площади крыши?

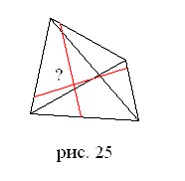
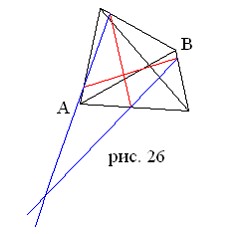
    3. На рис. 25 изображена треугольная пирамида, в которой проведены два отрезка, соединяющие точки на его противоположных ребрах. Можно ли по рисунку определить пересекаются эти отрезки в пространстве или нет? А если можно, то как?

    Решение задач

    1.

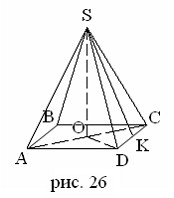
    Дано: SABCD – правильная четырехугольная пирамида; SO – высота; SO = 150 м; SA – боковое ребро; SA = 220 м;

    Найти: VSABCD; Sбок

    Решение: V = 1/3SABCD SO; Sбок = p∙SK/2

    Рассм. ∆SOC (O = 90˚)

    По теореме Пифагора: OC = √SC2 – SO2 = √2202 – 1502 = √48400 – 22500 = √25900 (м) ≈ 161 м

    т.к. ABCD – правильный прямоугольник, то: AB = OC√2 = √25900*2 = √51800 (м) ≈ 228 (м)

    Рассм. ∆ SCD (SC = CD = SD)

    CK = ½ CD; CK = 228/2 = 114 (м)

    Рассм. ∆SKC (K = 90˚)

    По теореме Пифагора: SK = √SC2 – CK2; SK = √2202 – 1142 = √48400 – 12996 = √35404 ≈ 188 (м)

    Периметр основания: p = 4∙228 = 912 (м)

    Находим Sбок = 4∙228∙114/2 = 51984 (м2)

    Sосн = AB2; Sосн = 2282 = 51984 (м2)

    Находим V = 1/3SABCD SO = 1/3∙51984∙150 = 2599200 (м3)

    Ответ: 51984 м2; 2599200 м3.

    2.

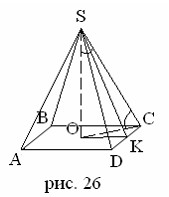
    Дано: SABCD – Правильная четырехугольная пирамида. AB = BC = 4,5 м SCO = 45˚; размеры листа: 70 см × 140 см; отходы: 10%

    Найти: N

    Решение: N = (Sбок + Sотх )/Sлиста

    Sбок = 4∙S∆CSD =4 ½ CD∙SK = 2CD∙SK

    Рассм. ∆SOC (O = 90˚; С = 45˚)

    т.к. сумма углов в треугольнике равна 180˚, то S = 180˚ – 90˚ – 45˚ = 45˚ → SO = OC

    т.к. ABCD – правильный четырехугольник, то OK = CD/2 = 4,5/2 = 2, 25 (м)

    Рассм. ∆OKC (K = 90˚; OK = CK)

    По теореме Пифагора: OC = √2OK2 = √2∙5, 0625 ≈ 3, 2 (м) → SO = 3, 2 (м)

    Рассм. ∆SOK (O = 90˚)

    По теореме Пифагора: SK = √SO2 + OK2 = √10, 24 + 5, 0625 = √15, 3 ≈ 3, 9 (м)

    Sбок = 2∙4, 5∙3, 9 = 35, 1 (м2)

    Sотх = Sбок∙0, 1 = 35, 1∙0, 1 = 3, 51 (м2)

    Sлиста = 0, 7∙1, 4 = 0, 98 (м2)

    N = (35, 1 + 3, 51)/0, 98 = 40

    Ответ: 40 листов

    3. Можно. Отрезки пересекаются (т.е. лежат в одной плоскости) тогда и только тогда, когда либо точка пересечения синих прямых лежит на прямой AB, либо они параллельны.

    Заключение

    Я рассмотрела большую тему о пирамидах, прочитала массу литературы об этих замечательных фигурах. Эта тема вызвала у меня неподдельный интерес. Я подробно рассмотрела элементы пирамиды, изучила основные свойства, решила множество задач на нахождение площади боковой поверхности и объема пирамиды.… Но это, конечно, не предел моего рассмотрения, на этом невозможно поставить точку. Во-первых, потому, что можно найти еще множество различной литературы по этой теме, а во-вторых, исследования пирамид продолжаются и сегодня. Этим занимаются ученые США, Японии, ФРГ и других государств. Ученые всех специальностей: астрономы и математики, химики и врачи, генетики и геронтологи – пытаются разгадать тайну пирамид и более подробно изучить их свойства.

    Пирамида имеет широкое применение в строительстве домов, различных сооружений. Я думаю, что я в жизни столкнусь еще не раз с этой фигурой, и круг моих знаний будет расширен. Советую учащимся интересоваться не только элементарными сведениями о пирамиде, но и изучать их глубже, что и сделала я.

    Список использованной литературы

    1. Аксёнова М.Д. Энциклопедия для детей. М.: «Аванта +», 2000.
    2. Антонов В.Ф. Биофизика. М.: «Владос», 2000.
    3. Барыбин Н.А. Геометрия: Учебник для 10 – 11, М.: Просвещение, 1986.
    4. Димде М. Целительная сила пирамид, М.: изд. Гранд, 2000.
    5. Киреев А. Лечебные пирамиды: возможное и действительное. М.: Просвещение, 2000.
    6. Погорелов А.В. Геометрия: Учебник для 7-11, 5-е изд. М: Просвещение, 1996.
    7. Савин А.П. Энциклопедический словарь юного математика. М.: Просвещение, 1985.
    8. Шарыгин И.Ф. Факультативный курс по математике. XI класс. М.: Просвещение, 1991.
    9. Штангл Ф. Маятник, рамка, сенсор. С-Петербург: Питер, 1999.
    

    Подобные работы:

    Актуально: