Физико-топологическое моделирование структур элементов БИС

Физико-топологическое моделирование

структур элементов БИС

Физико-топологическое моделирование структур элементов БИС является неотъемлемой составной частью современных САПР БИС. На этапе проектирования моделирование элементной базы позволяет решить вопросы, связанные с оптимизацией структурных и топологических решений интегральных структур элементов БИС для достижения максимальной плотности компоновки, максимального быстродействия и минимальной потребляемой мощности. Методы анализа и соответствующее прикладное математическое обеспечение являются основным инструментом разработчика современных БИС и СБИС. Физико-топологическое моделирование основано на использовании математических моделей, численных методов решения дифференциальных уравнений с учетом результатов расчета и экспериментальных данных. Физико-математическую основу моделирования интегральных компонентов составляют фундаментальные уравнения переноса электронов и дырок в полупроводниках. Непосредственно эти уравнения ввиду чрезвычайной сложности и громоздкости их численного интегрирования имеют ограниченное применение. Это делает невозможным решение задачи проектирования интегральных элементов на единой модельной и алгоритмической основе и приводит к необходимости ее разделения на более простые задачи. В настоящее время в практике проектирования используется большое число простых и экономичных моделей, эффективных для определенных типов элементов, а также для конкретных этапов их проектирования. Эти модели отличаются принятыми допущениями, размерностью, системами независимых переменных, видами краевых задач и алгоритмами их решения. Для эксплуатации программ и интерпретации полученных результатов необходимо прежде всего понимание используемых моделей, поэтому в данном учебном пособии значительное внимание уделяется выводу основных модельных уравнений. Принятая последовательность изложения позволяет овладеть основами физико-топологического моделирования, а не просто дает определенную сумму знаний.

Основные задачи моделирования

интегральных структур. Уровни моделирования

В связи с постоянной разработкой новой элементной базы БИС необходимы методы модели ования позволяющие посредством численных экпиpементов на ЭВМ устанавливать количественные зависимости между электрофизическими, топологическими паpаметрами интегpальных стpуктуp и множеством их эксплуатационных параметpов с учетом сложных взаимодействий в конкретных БИС. При этом решаются основные задачи: 1) исследование физических процессов в технологических установках; 2) исследование физических процессов в объеме и на поверхности интегральных структур при внешних воздействиях; 3) исследование электрических взаимодействий полупроводниковых приборов в составе БИС. Моделирование физических процессов в технологических установках позволяет получить, в частности, количественные характеристики пол п оводниковых интегpальных стpуктур. Таким характеристикам прежде всего относятся распределение концентраций легирующих примесей в эпитаксиальныхп ионно-легированных и диффузионных слоях, толщины таких слоев и другие электpофизические параметpы. Они являются исходными данными для проектирования элементов БИС. Следует отметить, что моделирование технологических процессов является важным, но не единственным источником данных, которые используются на следующем этапе проектирования.

Моделирование физических процессов в интегральных структурах элементов необходимо для: 1) исследования физики процессбв, протекающих в принципиально новых элементах БИС; 2) исследования новых конструктивно-технологических вариантов компонентов (в частности, компонентов с субмикронными размерами) и экстремальных режимов их работы; 3) определения параметров эквивалентных электрических схем. В результате должны быть определены структурные и топологические параметры элементов БИС. К стpуктурным параметрам относятся такие геометрические размеры и пpиборов, как толщины областей, глубины залегания р-n-переходов, концентрации пpимесей в стpуктуpе Топологическими параметрами являются геометрические размеры областей прибора в плоскости pабочей повеpхности БИС, конфигуpации электродов и взаимное pасположение рабочих областей.

Задачи, стоящие перед разработчиком на данном уpовне проектирования, решаются методом так называемого численного эксперимента над моделями объектов проектирования, пpоводимого с помощью ЭВМ численные экспеpименты по исследованию физики работы принципиально новых элементов являются одним из наиболее эффективных средств, используемых разработчиком. Альтернативой численному эксперименту в данном случае является технологический эксперимент. Однако технологические эксперименты сопряжены с большими затратами средств и времени.

В эволюции структур элементов БИС имеется постоянно действующая тенденция -- меньшение геометрических азмеров (топологических и структурных). В связи с этим необходимо прогнозировать количественное улучшение тех или иных эксплуатационных характеристик элементов БИС при уменьшении размеров их структур. Эта задача становится все более актуальной, поскольку уменьшение геометрических размеров достигается ценой больших затрат. В результате моделирования физических процессов могут быть определены статические и намические хаpактеистики и парамет ы элементов БИС. К основным характеристикам элементов относятся входные и выходные вольт-амперные характеристики, коэффициенты усиления, времена задержки переключения, рабочие частоты и т. п. Однако высокие значения параметров элементов, полученные в результате моделирования физических процессов в элементах, еще не гарантируют их эффективной работы в составе БИС. Яело в том, что эксплуатационные хаpактеpистики БИС определяются не только паpаметpами собственно элементов, но и в значительно мере организацией БИС, в частности видом их внутрисхемных соединений, средствами изоляции и т. п.

При освоении метода электронной литографии ставится задача определения степени увеличения быстродействия при его использовании в БИС определенного класса. Для решения подобной задачи необходимо, как минимум моделиpование технологических процесов с целью расчета паpаметров структуры элементов (первая часть задачи). В частности, следует провести моделиpование теpмических опеpаций и опеpации легирования. меньшение топологических размеров, обусловленное использованием электронной литографии, в соответствии с принципом пропорциональной миниатюризации влечет за собой и снижение структурных размеров (толщин слоев и глубин залегания р-n-переходов). Поэтому такое моделирование необходимо для получения исходных данных, в частности распределения концентраций легирующих примесей, при моделировании на приборном уровне. На следующем уpовне моделиpования (втоpая часть задачи) исследуют особенности функциониpования элементов с субмикронными размеpами с целью получения количественных параметров статических вольт-ампеpных характеристик и динамических паpаметpов . Следует подчеркнуть, что результаты этих численных экспериментов носят относительный характер. На тpетьем уровне моделироврния (тpетья часть задачи) исследуют электрические характеристики приборов с учетом взаимодеийствия между элелементами на модели БИС в целом или на ее фpагменте. Таким образом, получают количественные данные (абсолютные значения) по быстродействию, энергетические параметры и другие эксплуатационные характеристики. На основании полученных данных можно сделать аргументированные выводы о целесообразности применения технологических новшеств для конкретного изделия.

Иеpаpхическая система моделей,

используемых в САПР элементов БИС

Сложившееся в практике проектирования разделение труда между разработчиками БИС, с одной стороны, и учет реальных возможностей современных ЭВМ -- с другой, диктуют иной метод моделирования. Общепринятым в настоящее время является метод, согласно которому на азличных у овнях модели гния используют различные модели. Это о еспечивает достижение разумного компромисса: сложность модели -точность моделирования. Кроме того, такой метод позволяет достаточно гибко и оперативно проводить сравнение результатов моделирования с экспериментальными данными и уточнять исходные значения, т. е. осуществлять итерационный процесс оптимизации приборных структур по электpофизическим параметpам с учетом заданных электрических паpаметpов, пpинятых огpаничений. Этот метод позволяет также соразмерять возможности численного моделирования по точности с точностью исходных данных. В условиях резкого увеличения размерности задач, характерного для этапа создания СБИС и УБИС, главной тенденцией развития методов моделирования стало совмстное пpименения моделей различных иерархических уровней. Идея многоуровневого моделирования структур элементов БИС подразумевает комплексное использование при проектировании различных моделей одного и того же объекта -полупроводникового прибора транзисторного типа. На этапе технологического молелирования применяют модели, имитирующие процессы ионного легирования диффузии, эпитаксиального (гомо, гетеpо, молекуляpного) наращивания и оксидиpования. Именно эти процессы в основном определяют распределение примесей в полупроводниковых структурах, глубины и конфигурации р-n-переходов. Кроме этих моделей используют модели процессов формирования поверхностных конфигураций (топологии). Такими моделями являются модели литогpафии, исключающие нанесение и тpавление пленок. Исходными данными для моделирования являются параметры режимов соответствующего технологического оборудования (время обработки, температура, наружнос давление, доза и энергия ионной бомбардировки и т. п. ) Общее назначение моделей технологических пpоцессов -- модели планарной технологии создания БИС -- состоит в получении информации о конфигуpации и pазмеpах областей, распределении примесей в полупроводниковой структуре. На основании этой информации по известным зависимостям опpеделяют элекpтpофизические параметры отдельных рабочих областей сpтуктуры, ырпример подвижность, время жизни носителей, скорость рекомбинации и т. п. Как объект моделиpовадця полупроводниковыи при- бор представляет собой тpехмеpную структуpу из полуоводниковых; диэлектрических и металлических областей со сложным распределением концентраций легиpующих примесеи и с различными электpофизическими паpаметpами Кроме того, особенностью объекта моделирования является множество физических процессов, протекающих в его структуре, и сложный характер взаимодействия с окружающей средой. Исходя из задач пpоектирования элементной базы в качестве основных определены следующйе классы моделей интегральных структур: 1) стpктуpно-физические 2) физико-топологические, 3) электpические. Совокупность моделей образует систему, взаимосвязи в которой определяются иерархическим принципом. Модели, используемые на каждом последующем более высоком уровне проектирования, отличаются большей степенью абстрагирования. Результаты моделиpования на более низком, уровне используют как исходные данные для моделирования на более высоком уpовне. Для каждого уровня характерны своя теоретическая основа и математический аппарат для синтеза и анализа моделей. На пеpвом уpовне моделиpование производят наиболее детально. Hа основе феноменологической теоpии полупроводников рассматривают физические процессы в полуоворниковой структуpе: дрейф, диффузию, генерацию и рекомбинацию основных и неосновных носителей заряда. Исходными данными являются структурно-технологические параметры (геометрия структуры и распределение концентрации примесей в ней). В pезультате моделирования получают пространственно-временные распpеделения подвижных носителей заряда и электрического потенциала в стpуктуpе.

На втоpом уpовне моделирования полупроводниковых структур используются модели с меньшей детализацией. На основе теоpии поля с распределенными источниками тока рассматривают процессы растеканйя токов основных носителей заряда в рабочих областях элементов (тpанзисторных, функционально-интегрированных элементах, резисторах и т. п. ). Исходными данными для такого моделирования являются топология и так называемые интегральные параметры физической структуры, инвариантные относительно топологии. К таким параметрам относятся удельные значеия объемных и поверхностных сопротивлений рабочйх областеи, канальные токи р-п пеpеходов, барьерных и диффузионйых областеи. Эти параметры могут быть определены на первом уровне моделиpования или же экспеpиментально с помощью специальных тестовых элементов. Модели второго уровня, использующие уже найденные с помощью сложных физических моделей первого уровня интегральные параметры физической структуры, экономят машинное время по сравнению с моделями первого уровня за счет исключения вычислений пространственного распределения носителей заряда на каждом шаге итерационного процесса отработки топологии элементов. По существу, применение моделей второго уровня делает реальным автоматизацию процесса разработки топологии элементов за счет разделения задачи боль шой размерности, непосильной для современной вычислительной техники.

Таким образом, модели данного уровня, используются в качестве исходных данных результаты моделирования на первом уровне, позволяют с помощью ЭВМ опpеделить параметры электрических эквивалентных схем. Математическим аппаратом анализа на данном уровне являются численйые методы решения дифференциальных уравнений в частных производных в основе которых лежит метод конечных pазностей. Модели тpетьего уровня представляют собой обширную группу электрических эквивалентных схем. Эквивалентные схемы полупpоводниковых пpибоpов широко используют для pасчета элекpических режимов БИС. Теоретической основои для синтеза данного класс моделей являются модели первого уровня, применяемые и для идентификации некоторых параметров эквивалентных схем. Другой основой синтеза электрических эквивалентных схем и средством идентификации их параметров являются физико-топологические модели. В этом случае появляется возможность учета в эквивалентных схемах конкретной топологии элементов БИС. Кроме того, разработаны методы идентификации параметров эквивалентных схем по экспериментальным ВАХ. Результатом моделирования является нахождение токов и напряжений в ветвях и узлах принципиальной электрической схемы БИС илй ее фрагментов. Данные модели являются практически единственным аппаратом оценки эффективности того или иного схемотехнического решения БИС или ее отдельных фрагментов с учетом особенностей физической структуры и топологии. В конечном счете от точности данных моделей зависит точность прогнозирования электрических характеристик БИС.

Общие положения математической

формулировки задач моделирования

элементов БИС

Основным этапом первых двух уровней моделирования является математическая формулировка задачи. Эта процедура включает вывод уравнении, описывающих основные физические процессы внутри структуры прибора, и граничных условий. Последние пpедставляют собой математическйе зависимости, хаpактеpизующие процессы, происходящие на поверхности структуры. Эти зависимости имеют большое значение для моделирования, так как они отражают взаимодействие прибора с окружающей средой. Формулировке математической модели объекта предшествует ранжирование учитываемых факторов, процессов и эффектов и выбор приближений, от которых зависят сложность и эффективность модели. При этом выбирают конфигурацию и геометрические размеры модельной области, аппроксимируют распределения концентрации легирующих примесей в ней, обосновывают пренебрежения второстепенными физическими процессами и эффектами. Hа нижнем стpуктуpно-физическом уpовне объект моделирования, в общем случае являющийся трехмеpной полупроводниковои структурой, представляют можетвом плоских сечении, нормальных и параллельных плоскости pабочеи поверхности БИС. Множество сечений для ормирования модельных объектов выбирают на основании качественного анализа физических процессов в интегральной структуре элементов БИС. Эти сечения должны совпадать с плоскостями, в которых развиваются основные физические процессы, характеризующие работу прибора. Число сечений зависит от требуемой детализации учитываемых факторов, процессов и эффектов. Конфигурации моделей областей опpеделяют в пpеделах этих сечений. Hа pисунке изобpажена стpуктуpа базового элемента БИС И2Л-типа.

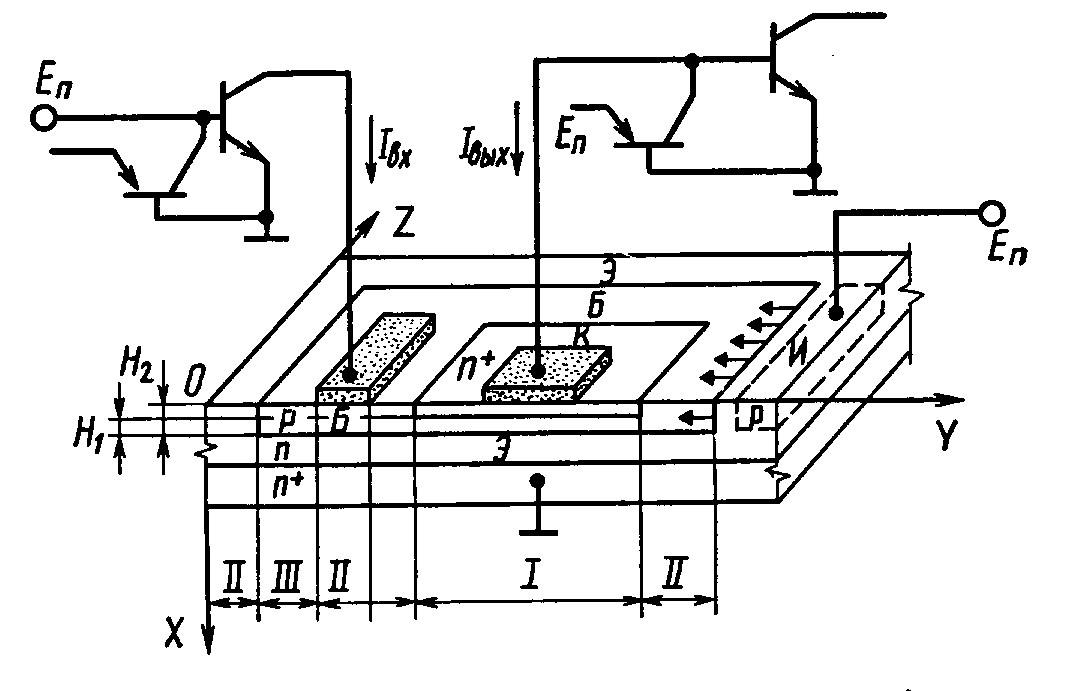
Физико-топологические модели элементов БИС

Основные требования и допущения

Физико-топологические модели должны:

1) просто и гибко учитывать топологию элементов БИС, в частности функционально-интегрированных (ФИЭ);

2) учйтывать в интегральной форме наиболее существенные физические процессы, олределяющие функционирование элементов БИС;

3) допускать стыковку по входам и выходам с электрическими эквивалентными системами, имитирующими условия работы элементов в составе БИС;

4) предполагать возможность моделирования фрагментов БИС с различной степенью приближения. Остановимся на каждом из перечисленных требований более подробно. Из первого требования следует, что модель должна быть в общем случае двумерной как для токов основных, так и неосновных носителей заряда в полупроводнике. При этом получается слишком громоздкая для практического проектирования модель.

Однако специфика архитектуры ФИЭ позволяет упростить задачу, ограничившись учетом двумерного характера токов только основных носителей заряда. Второе требование необходимо учитывать по следующим причинам. Во-первых, теоретически не представляется возможным разделить влияние на электрические параметры собственных конструктивных элементов и параметров окружающих элементов БИС. Во-вторых, общепризнанным является имитация условий работы

ФИЭ в составе БИС с помощью элементов электрических эквивалентных схем. Интегральный учет сложных физических процессов представляется практически единственным способом использования для проектирования полученных во время исследований экспериментальных данных и теоретических зависимостей. Именно такой подход позволит, не углубляясь в физику процессов, учесть их влияние на электрические параметры. Кроме того, возможность представления различных областей . в модели с произвольной степенью приближения практически необходима из экономических соображений. Отражая процессы, происходящие в плоскости, параллельной рабочей поверхности БИС, в то же время модель должна учитывать конкретный технологический процесс, характеризующийся определенными профилями примесей. В pазpабатываемой модели должны учитываться вре физические процессы, имеющие место в pеальной стpуктуре пpи различных pежимах работы. Эта задача может быть оптимально решена только в том случае, когда природа конкретного эффекта не будет идентифицироваться, а его реальное проявление, которое зависит от технологического процесса, будет вместе с другими существенными в этом режиме эффектами учтено в аппроксимациях соответствующих параметров. Эти параметры должны быть получены экспериментально или с помощью машинного эксперимента. Недостаток такого <не физичного> подхода заключается в возможной избыточности параметров модели, описывающих этот эффект. Неоспоримым его преимуществом при данной постановке задачи является универсальностъ и достаточная точность отображения любого сочетания классических (Эрли, Вебстера, Кирка и т. п. ) и неклассических эффектов (прозрачность эмиттера, вытеснение тока к периферии эмиттера и т. п. ) в реальной структуре при любом вырождении областей полупроводниковой структуры и уровне инжекции. Таким образом, разрабатываемая модель должна позволять моделировать основные биполярные структуры на основе единого подхода, т. е. изменение топологии не должно вызывать изменения самой модели и должно отражаться лишь в пересчете каких-либо ее параметров, отражающих новые границы. В этом смысле модель должна быть инвариантна (неизменна) относительно топологии, Методы определения параметров модели должны быть по возможности экономичными (ограниченное число тестовых структур) и полными, т. е. позволяк)щими рассчитать все необходимые параметры модели для любых вариантов топологии. Поэтому синтез модели удобно начать с рассмотрения электрофизических характеристик основных конструктивных компонентов общих для всех планарных биполярных функционально-и нтегрированных полупроводниковых структур. Анализ показывает, что независимо от схемотехнической организации можно выделить ряд основных конструктивных компонентов, общих для большинства функционально-интегрированных биполярных структур и достаточных для их построения.

Этими основными компонентами являются:

а) выпрямляющие р-n-переходы (или переходы типа Шотки), имеющие активные (инжектирующие, коллектирующие или совмещающие эти функции) и пассивные участки;

б) активные полупроводниковые области, в которых происходят генерация, рекомбинация, дрейф, диффузия неосновных и дрейф основных носителей заряда;

в) пассивные полупроводниковые области, в которых осуествляется дрейф основных носителей заряда;

г) полэлектродные области (области омических контактов).

Общая характеристика методов

моделирования

Основным подходом к построению практических моделеи интегральных структур является упрощение общей математической модели с учетом особенностей конкретных типов приборов. При этом используют различные предпосылки для основных физических процессов, обусловливающих функционирование приборов. Для каждого типа прибора выявляют основные физические процессы, что позволяет из общей системы уравнений выделить уравнения, олисывающие эти физические процессы в характерных активных областях структуры. Например, для биполярного транзистора такой активной областью является база, для полевого -- канал. Процессы, протекающие в базовой области при низких и средних уровнях инжекции, достаточно точно описываются уравнением непрерывности для неосновных носителей заряда, а процессы, протекающие в канальной области, -уравнениями непрерывности и Пуассона. При этом из структуры прибора выделяют активные области, а из общей системы -- уравнения, характеризующие эти области. Остальные рабочие области приборов и соответствующие им уравнения из рассмотрения исключают. Выделенные уравнения подвергаются упрощениям для приведения их к виду, поддающемуся аналитическому решению. Типичными упрощениями такого рода являются: приведение к одномерному виду, простые аппроксимации (например, равномерного или экспоненциального) распределения примесей, использование условии низкого уровня йнжекции и стационарного режима, представление границ областей пространственного заряда и квазинейтральных областей ступенчатыми и т. п. Рассмотренный метод предусматривает любые упрощения уравнений с целью их аналитического решения. Полученные решения и являются аналитическими моделями приборов, справедливыми лишь для частных случаев. Как правило, данный вид моделей можно использовать для одномерных областей или одномерных участков реальных двумерных областей. В общем случае для приборных структур элементов БИС аналитические модели получить не удается. Поэтому основным типом моделей являются алгоритмические, из которых можно выделить два класса, отличающиеся по способу выделения модельных областей. Первый предусматривает, так же как и аналитические модели, расчленение структуры на области (регионы), второй рассматривает прибор как единое целое. Таким образом, аналитические модели и первый класс алгоритмических моделей объединяет общий подход, который включает в себя приближенные методы, получившие название метода региональных приближений. Классу моделей, не предусматривающему выделение активных областей в приборе, соответствуют прямые методы решения системы уравнений переноса, алгоритм Гуммеля и его многочисленные модификации. При этом полупроводниковая структура рассматривается в целом и для нее анализируется полная система уравнений переноса. Алгоритмические методы в силу упомянутых математических трудностей допускают лишь численные методы решения. Таким образом, все используемые в практике проектирования модели относятся или к методу региональных приближений, или к прямым методам решения.

Метод региональных приближений

К моделям элементов БИС, используемым при автоматизированном проектированйи, предъявляют два пpотиворечивых требования -- они должны быть точными и экономичными. В ряде случаев компромисс может быть достигнут путем введения физически оправданных упрощений математических моделей. Одним из наиболее эффективных компромиссных подходов такого рода является метод региональных приближений. Метод предусматривает разбиение транзитной структуры на отдельные области, совпадающие с областями пространственного заряда (ОПЗ) р-п-переходов и квазинейтральными областями. При этом появляется возможность производить расчет полупроводникового прибора по частям. Расчет отдельных областей и сшивка полученных решений на границах составляет один цикл итерационного процесса решения. Экономичность моделирования при таком подходе может быть достигнута за счет того, что для отдельных областей решают не полную систему уравнений, а лишь отдельные уравнения.