Метод Дэвидона - Флетчера - Пауэлла
Министерство науки, высшей школы и технической
политики Российской Федерации.
Новосибирский Государственный
Технический Университет.

Реферат по исследованию операций на тему
«Метод Дэвидона - Флетчера - Пауэлла».
Вариант №2.
Факультет: АВТ.
Кафедра: АСУ.
Группа: АС-513.
Студент: Бойко Константин Анатольевич.
Преподаватель: Ренин Сергей Васильевич.
Дата: 19 октября 1997 года.
Новосибирск
Введение.
Первоначально метод был предложен Дэвидоном (Davidon (1959) ), а затем развит Флетчером и Пауэллом (Fletcher, Powell (1963) ). Метод Дэвидона - Флетчера - Пауэлла называют также и методом переменной метрики. Он попадает в общий класс квазиньютоновских процедур, в которых направления поиска задаются в виде -Dj![]() f(y). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj , где Dj - положительно определенная симметрическая матрица порядка n х n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj+1 представляется в виде суммы Dj и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два.
f(y). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj , где Dj - положительно определенная симметрическая матрица порядка n х n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj+1 представляется в виде суммы Dj и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два.
Алгоритм Дэвидона - Флетчера - Пауэлла.
Рассмотрим алгоритм Дэвидона - Флетчера - Пауэлла минимизации дифференцируемой функции нескольких переменных. В частности, если функция квадратичная, то, как будет показано позднее, метод вырабатывает сопряженные направления и останавливается после выполнения одной итерации, т.е. после поиска вдоль каждого из сопряженных направлений.
Начальный этап.
Пусть ![]() >0 - константа для остановки. Выбрать точку х1 и начальную симметрическую положительно определенную матрицу D1. Положить y1 = x1, k = j = 1 и перейти к основному этапу.
>0 - константа для остановки. Выбрать точку х1 и начальную симметрическую положительно определенную матрицу D1. Положить y1 = x1, k = j = 1 и перейти к основному этапу.
Основной этап.
Шаг 1. Если ||![]() f(yj) ||< ε, то остановиться; в противном случае положить dj = - Dj
f(yj) ||< ε, то остановиться; в противном случае положить dj = - Dj![]() f(yj) и взять в качестве λj оптимальное решение задачи минимизации f(yj + λdj) при λ ≥ 0. Положить yj+1 = yj + λjdj. Если j < n, то перейти к шагу 2. Если j = n, то положить y1 = xk+1 = yn+1, заменить k на k+1, положить j=1 и повторить шаг 1.
f(yj) и взять в качестве λj оптимальное решение задачи минимизации f(yj + λdj) при λ ≥ 0. Положить yj+1 = yj + λjdj. Если j < n, то перейти к шагу 2. Если j = n, то положить y1 = xk+1 = yn+1, заменить k на k+1, положить j=1 и повторить шаг 1.
Шаг 2. Построить Dj+1 следующим образом :
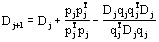 , (1)
, (1)
где
pj = λjdj, (2)
qj = ![]() f(yj+1) -
f(yj+1) - ![]() f(yj). (3)
f(yj). (3)
Заменить j на j + 1 и перейти к шагу 1.
Пример.
Рассмотрим следующую задачу :
минимизировать (x1 - 2)4 + (x1 - 2x2)2.
Результаты вычислений методом Дэвидона - Флетчера - Пауэлла приведены в таблице 1.
Таблица 1. Результаты вычислений по методу Дэвидона - Флетчера - Пауэлла.
k | xk f(xk) | j | yj f(yj) |
| || | D | dj | λj | yj+1 |
1 | (0.00, 3.00) (52.00) | 1 2 | (0.00, 3.00) (52.00) (2.70, 1.51) (0.34) | (-44.00, 24.00) (0.73, 1.28) | 50.12 1.47 |
| (44.00, -24.00) (-0.67, -1.31) | 0.062 0.22 | (2.70, 1.51) (2.55, 1.22) |
2 | (2.55, 1.22) (0.1036) | 1 2 | (2.55, 1.22) (0.1036) (2.45, 1.27) (0.0490) | (0.89, -0.44) (0.18, 0.36) | 0.99 0.40 |
| (-0.89, 0.44) (-0.28, -0.25) | 0.11 0.64 | (2.45, 1.27) (2.27, 1.11) |
3 | (2.27, 1.11) (0.008) | 1 2 | (2.27, 1.11) (0.008) (2.25, 1.13) (0.004) | (0.18, -0.20) (0.04, 0.04) | 0.27 0.06 |
| (-0.18, 0.20) (-0.05, -0.03) | 0.10 2.64 | (2.25, 1.13) (2.12, 1.05) |
4 | (2.12, 1.05) (0.0005) | 1 2 | (2.12, 1.05) (0.0005) (2.115, 1.058) (0.0002) | (0.05, -0.08) (0.004, 0.004) | 0.09 0.006 |
| (-0.05, 0.08) | 0.10 | (2.115, 1.058) |
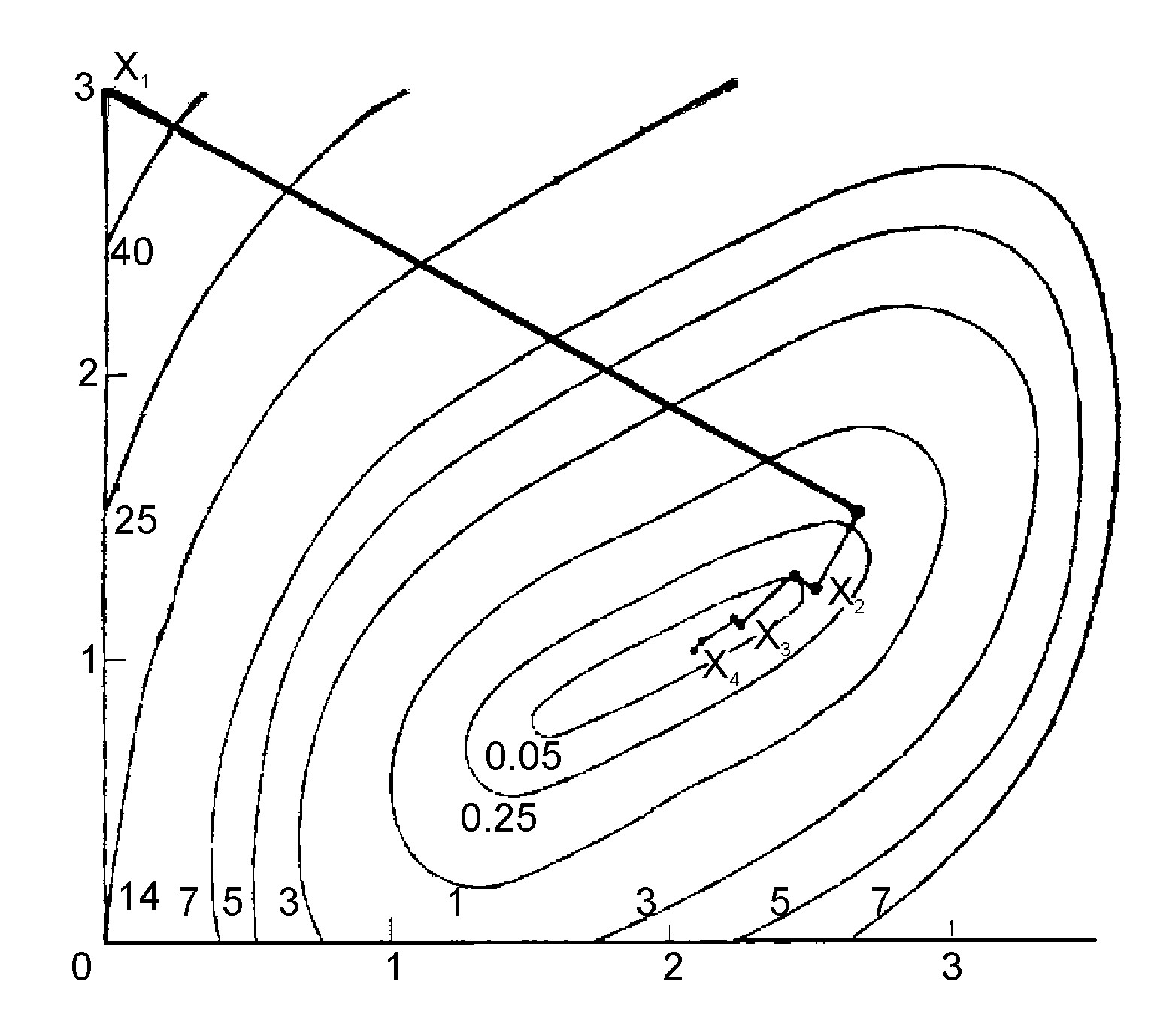
На каждой итерации вектор dj для j = 1, 2 определяется в виде–Dj![]() f(yj), где D1 – единичная матрица, а D2 вычисляется по формулам (1) - (3). Приk = 1 имеем p1 = (2.7, -1.49)T, q1 = (44.73, -22,72)T. На второй итерацииp1 = (-0.1, 0.05)T, q1 = (-0.7, 0.8)T и, наконец, на третьей итерацииp1 = (-0.02, 0.02)T, q1 = (-0.14, 0.24)T. Точка yj+1 вычисляется оптимизацией вдоль направления dj при начальной точке yj для j = 1, 2. Процедура остановлена в точкеy2 = (2.115, 1.058)T на четвертой итерации, так как норма ||f(y2) ||= 0.006 достаточно мала. Траектория движения, полученная методом, показана на рисунке 1.
f(yj), где D1 – единичная матрица, а D2 вычисляется по формулам (1) - (3). Приk = 1 имеем p1 = (2.7, -1.49)T, q1 = (44.73, -22,72)T. На второй итерацииp1 = (-0.1, 0.05)T, q1 = (-0.7, 0.8)T и, наконец, на третьей итерацииp1 = (-0.02, 0.02)T, q1 = (-0.14, 0.24)T. Точка yj+1 вычисляется оптимизацией вдоль направления dj при начальной точке yj для j = 1, 2. Процедура остановлена в точкеy2 = (2.115, 1.058)T на четвертой итерации, так как норма ||f(y2) ||= 0.006 достаточно мала. Траектория движения, полученная методом, показана на рисунке 1.
Рисунок 1. Метод Дэвидона - Флетчера - Пауэлла.
Лемма 1 показывает, что каждая матрица Dj положительно определена и dj является направлением спуска.
Для доказательства леммы нам понадобится :
Теорема 1. Пусть S - непустое множество в Еn, точка x ∈ cl S. Конусом возможных направлений в точке x называется множество D = {d : d ≠ 0, x + λd ∈ S при всех λ ∈ (0, δ) для некоторого δ > 0}.
Определение. Пусть x и y - векторы из Еn и |xTy| - абсолютное значение скалярного произведения xTy. Тогда выполняется следующее неравенство, называемое неравенством Шварца : |xTy| ≤ ||x|| ||y||.
Лемма 1.
Пусть y1 ∈ Еn, а D1 – начальная положительно определенная симметрическая матрица. Для j = 1, ..., n положим yj+1 = yj + λjdj, где dj = –Dj![]() f(yj), а λj является оптимальным решением задачи минимизации f(yj + λdj) при λ ≥ 0. Пусть, кроме того, дляj = 1, ..., n – 1 матрица Dj+1 определяется по формулам (1) - (3). Если
f(yj), а λj является оптимальным решением задачи минимизации f(yj + λdj) при λ ≥ 0. Пусть, кроме того, дляj = 1, ..., n – 1 матрица Dj+1 определяется по формулам (1) - (3). Если ![]() f(yj) ≠ 0 дляj = 1, ..., n, то матрицы D1, ..., Dn симметрические и положительно определенные, так что d1, ..., dn – направления спуска.
f(yj) ≠ 0 дляj = 1, ..., n, то матрицы D1, ..., Dn симметрические и положительно определенные, так что d1, ..., dn – направления спуска.
Доказательство.
Проведем доказательство по индукции. При j = 1 матрица D1 симметрическая и положительно определенная по условию леммы. Кроме того, ![]() f(y1)Td1 = –
f(y1)Td1 = –![]() f(y1)TD1
f(y1)TD1![]() f(y1) < 0, так как D1 положительно определена. Тогда по теореме 1 вектор d1 определяет направление спуска. Предположим, что утверждение леммы справедливо для некоторого j ≤ n – 1, и покажем, что оно справедливо для j+1. Пусть x – ненулевой вектор из En, тогда из (1) имеем
f(y1) < 0, так как D1 положительно определена. Тогда по теореме 1 вектор d1 определяет направление спуска. Предположим, что утверждение леммы справедливо для некоторого j ≤ n – 1, и покажем, что оно справедливо для j+1. Пусть x – ненулевой вектор из En, тогда из (1) имеем
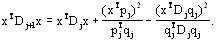 (4)
(4)
Так как Dj – симметрическая положительно определенная матрица, то существует положительно определенная матрица Dj1/2, такая, что Dj = Dj1/2Dj1/2. Пустьa = Dj1/2x и b = Dj1/2qj. Тогда xTDjx = aTa, qjTDjqj = bTb и xTDjqj = aTb. Подставляя эти выражения в (4), получаем :
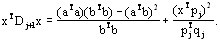 (5)
(5)
По неравенству Шварца имеем (aTa)(bTb) ≥ (aTb)2. Таким образом, чтобы доказать, что xTDj+1x ≥ 0, достаточно показать, что pjTqj > 0 и bTb > 0. Из (2) и (3) следует, что
pjTqj = λjdjT(![]() f(yj+1) –
f(yj+1) – ![]() f(yj)). (6)
f(yj)). (6)
По предположению![]() f(yj) ≠ 0, и Dj положительно определена, так что
f(yj) ≠ 0, и Dj положительно определена, так что![]() f(yj)TDj
f(yj)TDj![]() f(yj) > 0. Кроме того, dj – направление спуска, и, следовательно, λj > 0. Тогда из (6) следует, что pjTqj > 0. Кроме того, qj ≠ 0, и , следовательно, bTb= qjTDjqj > 0.
f(yj) > 0. Кроме того, dj – направление спуска, и, следовательно, λj > 0. Тогда из (6) следует, что pjTqj > 0. Кроме того, qj ≠ 0, и , следовательно, bTb= qjTDjqj > 0.
Покажем теперь, что xTDj+1x > 0. Предположим, что xTDj+1x = 0. Это возможно только в том случае, если (aTa)(bTb) = (aTb)2 и pjTx = 0. Прежде всего заметим, что(aTa)(bTb) = (aTb)2 только при a = λb, т.е. Dj1/2x = λDj1/2qj. Таким образом, x = λqj. Так как x ≠ 0, то λ ≠ 0. Далее, 0 = pjTx = λ pjTqj противоречит тому, что pjTqj > 0 и λ ≠ 0. Следовательно, xTDj+1x > 0, т.е. матрица Dj+1 положительно определена.
Поскольку ![]() f(yj+1) ≠ 0 и Dj+1 положительно определена, имеем
f(yj+1) ≠ 0 и Dj+1 положительно определена, имеем![]() f(yj+1)Tdj+1 = –
f(yj+1)Tdj+1 = –![]() f(yj+1)T Dj+1
f(yj+1)T Dj+1![]() f(yj+1) < 0. Отсюда по теореме 1 следует, что dj+1 – направление спуска.
f(yj+1) < 0. Отсюда по теореме 1 следует, что dj+1 – направление спуска.
Лемма доказана.
Квадратичный случай.
В дальнейшем нам понадобиться :
Теорема 2. Пусть f(x) = cTx + 1 xTHx, где Н - симметрическая матрица порядка n x n. Рассмотрим Н - сопряженные векторы d1, …, dn и произвольную точку x1. Пусть λk для k = 1, …, n - оптимальное решение задачи минимизацииf(xk + λdk) при λ ∈ Е1 и xk+1 = xk + λdk. Тогда для k = 1, …, n справедливы следующие утверждения :
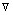 f(xk+1)Tdj = 0, j = 1, …, k;
f(xk+1)Tdj = 0, j = 1, …, k;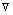 f(x1)Tdk =
f(x1)Tdk =  f(xk)Tdk;
f(xk)Tdk;- xk+1 является оптимальным решением задачи минимизации f(x) при условииx - x1 ∈ L(d1, …, dk), где L(d1, …, dk) – линейное подпространство, натянутое на векторы d1, …, dk, то есть
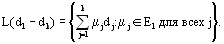 В частности, xn+1 – точка минимума функции f на Еn.
В частности, xn+1 – точка минимума функции f на Еn.
Если целевая функция f квадратичная, то в соответствии со сформулированной ниже теоремой 3 направления d1, …, dn, генерируемые методом Дэвидона - Флетчера - Пауэлла, являются сопряженными. Следовательно, в соответствии с утверждением 3 теоремы 2 метод останавливается после завершения одной итерации в оптимальной точке. Кроме того, матрица Dn+1, полученная в конце итерации, совпадает с обратной к матрице Гессе Н.
Теорема 3. Пусть Н – симметричная положительно определенная матрица порядка n x n. Рассмотрим задачу минимизации f(x) = cTx + 1 xTHx при условии x ∈ En. Предположим, что задача решена методом Дэвидона - Флетчера - Пауэлла при начальной точке y1 и начальной положительно определенной матрице D1. В частности, пусть λj, j = 1, …, n, – оптимальное решение задачи минимизации f(yj + λdj) при λ ≥ 0 и yj+1 = yj + λjdj, где dj = -Dj![]() f(yj), а Dj определяется по формулам (1) – (3). Если
f(yj), а Dj определяется по формулам (1) – (3). Если ![]() f(yj) ≠ 0 для всех j, то направленияd1, …, dn являются Н - сопряженными и Dn+1 = H-1. Кроме того, yn+1 является оптимальным решением задачи.
f(yj) ≠ 0 для всех j, то направленияd1, …, dn являются Н - сопряженными и Dn+1 = H-1. Кроме того, yn+1 является оптимальным решением задачи.
Доказательство.
Прежде всего покажем, что для j, такого, что 1 ≤ j ≤ n, справедливы следующие утверждения :
- d1, …, dj линейно независимы.
- djTHdk = 0 для i ≠ k; i, k ≤ j.
- Dj+1Hpk, или, что эквивалентно, Dj+1Hdk = dk для 1 ≤ k ≤ j, pk = λkdk.
Проведем доказательство по индукции. Для j = 1 утверждения 1 и 2 очевидны. Чтобы доказать утверждение 3, заметим прежде всего, что для любого k справедливы равенства
Hpk = H(λkdk) = H(yk+1 - yk) = ![]() f(yk+1) –
f(yk+1) –![]() f(yk) = qk. (7)
f(yk) = qk. (7)
В частности, Hp1 = q1. Таким образом, полагая j = 1 в (1), получаем
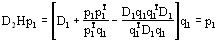 ,
,
т.е. утверждение 3 справедливо при j = 1.
Теперь предположим, что утверждения 1, 2 и 3 справедливы для j ≤ n – 1. Покажем, что они также справедливы и для j + 1. Напомним, что по утверждению 1 теоремы 2 diT![]() f(yj+1) = 0 для i ≤ j. По индуктивному предположению di = Dj+1Hdi, i ≤ j. Таким образом, для i ≤ j имеем
f(yj+1) = 0 для i ≤ j. По индуктивному предположению di = Dj+1Hdi, i ≤ j. Таким образом, для i ≤ j имеем
0 = diT![]() f(yj+1) = diTHDj+1
f(yj+1) = diTHDj+1![]() f(yj+1) = –diTHdj+1.
f(yj+1) = –diTHdj+1.
Ввиду предположения индукции это равенство показывает, что утверждение 2 также справедливо для j+1.
Теперь покажем, что утверждение 3 справедливо для j+1.
Полагая k ≤ j+1, имеем
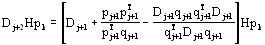 . (8)
. (8)
Учитывая (7) и полагая k = j + 1 в (8), получим, что Dj+2Hpj+1 = pj+1. Теперь пусть k ≤ j. Так как утверждение 2 справедливо для j + 1, то
pj+1THpk = λkλj+1dj+1THdk = 0. (9)
По предположению индукции из (7) и вследствие того, что утверждение 2 справедливо для j + 1, получаем
![]() . (10)
. (10)
Подставляя (9) и (10) в (8) и учитывая предположение индукции, получаем
![]() .
.
Таким образом, утверждение 3 справедливо для j+1.
Осталось показать, что утверждение 1 справедливо для j+1. Предположим, что ![]() . Умножая это равенство на
. Умножая это равенство на ![]() и учитывая, что утверждение 2 справедливо для j+1, получаем, что
и учитывая, что утверждение 2 справедливо для j+1, получаем, что ![]() . По условию теоремы
. По условию теоремы ![]() , а по лемме 1 матрица
, а по лемме 1 матрица ![]() положительно определена, так что
положительно определена, так что ![]() . Так как H положительно определена, то
. Так как H положительно определена, то ![]() и, следовательно,
и, следовательно, ![]() . Отсюда следует, что
. Отсюда следует, что ![]() , и так как d1, …, dj линейно независимы по предположению индукции, то
, и так как d1, …, dj линейно независимы по предположению индукции, то ![]() для i = 1, …, j. Таким образом, d1, …, dj+1 линейно независимы и утверждение 1 справедливо для j+1. Следовательно, утверждения 1, 2 и 3 выполняются. В частности сопряжённость d1, …, dn следует из утверждений 1 и 2, если положить j = n.
для i = 1, …, j. Таким образом, d1, …, dj+1 линейно независимы и утверждение 1 справедливо для j+1. Следовательно, утверждения 1, 2 и 3 выполняются. В частности сопряжённость d1, …, dn следует из утверждений 1 и 2, если положить j = n.
Пусть теперь j = n в утверждении 3. Тогда ![]() для k = 1, …, n. Если в качестве D взять матрицу, столбцами которой являются векторы d1, …, dn, то
для k = 1, …, n. Если в качестве D взять матрицу, столбцами которой являются векторы d1, …, dn, то ![]() . Так как D имеет обратную, то
. Так как D имеет обратную, то ![]() , что возможно только в том случае, если
, что возможно только в том случае, если ![]() . Наконец,
. Наконец, ![]() является оптимальным решением по теореме 2.
является оптимальным решением по теореме 2.
Теорема доказана.
Список литературы.
- Базара М., Шетти К. «Нелинейное программирование. Теория и алгоритмы». М., 1982.
- Химмельблау Д. «Прикладное нелинейное программирование». М., 1975.