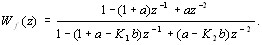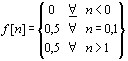Разработка и исследование системы автоматического регулирования и управления уровня жидкости
Техническое заданиена разработку и исследование системы
автоматического регулирования и управления
уровня жидкости в сборнике открытого типа.
Вариант 19
1. В сборниках открытого типа (рис.1) 1 как объект: управления уровнем жидкости, поступает расход жидкости Qn и вытекает из него жидкость Qo. Указанные расходы можно изменять с помощью регулирующего органа 2 и запорной задвижки 8. Уровень жидкости h должен стабилизироваться соответствующей автоматической системой.
Технические данные сборника:
- расход поступающей жидкости
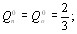
- уровень жидкости ho = 1 м;
- площадь поперечного сечения сборника
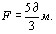
2. Передаточная функция сборника жидкости открытого типа (3)
| ( 1 ) |
где y(p) и u(p) - соответственно изображение по Лапласу уровня жидкости и управляющего воздействия; Ko и To - коэффициент усиления и постоянная времени сборника с объекта управления; p - оператор Лапласа.
Коэффициент усиления ![]()
Постоянная времени ![]()
3. Управляющий вычислительный комплекс (УВК) должен реализовать дискретный ПИ–регулятор, программирующая функция которого имеет вид – (1):
u(n) = u(n-1) + {k1 ∆y(n) - k2 ∆y(n-1)}, | ( 2 ) |
где ∆y(n) = g(n) - y(n) – рассогласование между заданным и текущим значением регулируемой переменной; k1 и k2 – коэффициенты настройки ПИ-регулятора.
4. Период дискретности системы управления Т = 5 с.
5. Исполнительный механизм принять мембранным, пневматическим.
6. Изменение во времени возмущающего воздействия, приведеный к выходу ∆y и имеет такой вид:
| ( 3 ) |
7. Изменение задающего воздействия
| ( 4 ) |
а также
| ( 5 ) |
8. Автоматическая система регулирования управления уровнем жидкости в сборнике открытого типа должна быть реализована на управляющем вычислительном комплексе ACBTГМ.
1. Разработка математической модели объекта управления.
На рис.1 приведена принципиальная схема сборника уровня жидкости как объекта управления уровнем жидкости.
Полная производная от объекта жидкости V может быть определена так
| (1.1) |
где V – объем жидкости в сборнике, м3;
Qn и Qo - соответственно расход подвижной и отводимой жидкости в сборник, м3/с, t – время, с.
Известно, что расход жидкости
| (1.2) |
Где f – площадь поперечного сечения запорной задвижки (вентиля), м2; h – уровень жидкости, м; g – ускорение силы тяжести, м/с2.
Подставив выражение (1.2) в уравнение (1.1) получим:
| (1.3) |
Полученное дифференциальное уравнение (1.3) является нелинейным и поэтому неудобным для дальнейшего исследования. Линеаризуем это уравнение т.е. записываем его в отношениях переменых:
| (1.4) |
Так как , ![]() , то
, то
| (1.5) |
Определим частные прозводные:
|
Или
| (1.6) |
| (1.7) |
Подставив выражения (1.6) и (1.7) в (1.5) получим
| (1.8) |
Подставив выражение (1.8) в уравнение (1.4), и записав ΔV=FΔh, получим следующее:
| (1.9) |
Дифференциальное уравнение (1.9) можно записать в более сжатой форме так:
То
| (1.10) |
где ![]() – постоянная времени объекта управления, с.
– постоянная времени объекта управления, с.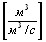 .
.
![]() – коэффициент усиления по каналу управления,
– коэффициент усиления по каналу управления, ![]() ;
;
![]() – коэффициент усиления по каналу возмущения, н/м2.
– коэффициент усиления по каналу возмущения, н/м2.
В операционной форме дифференциальные уравнения запишем так
(T0p+1) y(p) = K0 u(p) – Kf f(p), | (1.11) |
где p – оператор Лапласа; y(p), u(p) и f(p) – соответственно, изображения по Лапласу уровня жидкости, расхода подводимой жидкости, площади поперечного сечения запорной задвижки.
Итак, ![]()
![]()
![]()
Из выражения (1.11) определим передаточную функцию ОХУ по каналу управления (при ![]() )
)
| (1.12) |
- Разработка технической структуры системы управления.
ОУ – объект управления (сборник жидкости);
РО – регулирующий орган;
МИМ – мембранный исполнительный механизм;
УСД – устройство связи с объектом в составе:
- ПКТ – преобразователь «код-ток»;
- МГУ – модуль группового управления;
- МВДИ – модуль ввода дискретной информации;
- КССУ – комутатор сигналов среднего уровня;
- АЦП – аналого-цифровой преобразователь;
- МУК – модуль управления коммутаторами;
- ВВВ – расширитель ввода-вывода.
Как видно из рис.2 в САУ уровнем жидкости используется датчик уровня (ДУ) с пневматическим напором и пневматический мембранно-исполнительный механизм (МИМ). Поэтому в системе предусматриваются преобразователи сигналов: пневмоэлектрический (ПЭ-55м) и электропневматический (ЭПП-М).
3. Разработка алгоритмической структуры системы управления.
На рис.3 приведена алгоритмическая структура системы управления уровнем жидкости в сборнике жидкости с пневматическим исполнительным механизмом.
Определим численные значения параметра всех звеньев рассматриваемой САУ.
Передаточная функция ОУ согласно технического задания (ТЗ) определяется так:
| (3.1) |
Полагаем, что датчик уровня жидкости и пневматический электропреобразователь являются безынерцтонными звеньями, тогда передаточная функция
| (3.2) |
Дискретная передаточная система ввода и информации в УВК, т.е. совокупности программы и устройства ввода может быть представлена так:
Wв(z)=Kв | (3.3) |
В данном случае можно не определять численные значения коэффициентов передачи датчика, преобразователя к системе ввода ![]() , так как на входе и выходе совокупность этих звеньев имеет одну и ту же управляемую переменную. Следовательно, передаточная функция
, так как на входе и выходе совокупность этих звеньев имеет одну и ту же управляемую переменную. Следовательно, передаточная функция
| (3.4) |
Дискретную передаточную функцию программы, реализующей ПИ-закон управления, можно получить записав уравнение (21) с помощью оператора смещения (1). Тогда
(1 – z–1) u(n) = (K1 – K2 z–1)Δy(n) | (3.5) |
Или
| (3.6) |
Передаточную функцию системы вывода информации из УВК (совокупности программы и устройства вывода), можно принять как передаточную функцию фиксатора (экстраполятора) нулевого порядка:
Поэтому
| (3.7) |
Электропневматический преобразователь и исполнительный механизм будем считать безынерционными звеньями. Тогда передаточная функция
| (3.8) |
Коэффициенты передачи системы вывода информации, электропневмопреобразователя и исполнительного механизма можно не определять, так как на входе и выходе этой системы звенья имеют одно и то же значение управляющего воздействия. Следовательно, передаточная функция
| (3.9) |
Таким образом, общая передаточная функция непрерывной части системы (НЧС) имеет такой вид:
| (3.10) |
Или
| (3.11) |
В дискретной форме передаточная функция (3.11) примет такой вид
| (3.12) |
Где a = exp(-T/T0), b = K0 (1 - a).
То = 69 с,
Т = 5 с,
Ко = 21,
То
a = exp(-T/T0) = e-5/69 = 0,930;
b = K0 (1 - a) = 3(1 – 0,930) = 0,210.
Таким образом, алгоритмическая структура рассматриваемой системы примет вид, приведенный на рис.4.
4. Расчет области устойчивости.
Для определения параметров настроек (K1 и K2) ПИ-регулятора рассчитаем область устойчивости рассматриваемой системы. Для этого составим характеристические уравнения замнутой системы. Исходя из рис.4 имеем:
1 + Wупр (z) W0 (z) = 0. | (4.1) |
Подставив в это выражение выражение (3.5) и (3.11) получим:
| (4.2) |
Отсюда, после несложных преобразований, характеристическое уравнение примет вид:
z2 - (1 + a - K1b) z + (a - K2b) = 0. | (4.3) |
Для определения искомых параметров настроек (К1 и К2), при которых система устойчива, воспользуемся методом замены переменных (21). Подставляя в уравнение (4.3)
| (4.4) |
где ω - частота, рад./с.
Получим следующее:
(2 + 2a - K1b - K2b) ω + 2(1 – a + K2b) ω - K1b + K2b = 0. | (4.5) |
Условием устойчивости системы является отрицательность вещественной части корней уравнения (4.5). Для чего в соответствии с алгебраическим критерием устойчивости Рауса (3) должны выполняться следующие неравенства:
| (4.6) |
Отсюда вытекают следующие условия устойчивости системы (при a = 0,930, b = 0,210)
| (4.7) |
На рис.5 изображена область устойчивости САУ уровнем жидкости в сборнике жидкости открытого типа с ПИ-регулятором в плоскости настроек удовлетворяющих неравенствам (4.7).
5. Расчет качеста системы управления.
5.1. Расчет переходного процесса при изменении возмущающего воздействия.
Для расчета переходного процесса в системе при изменении возмущающего воздействия (рис.4) определим передаточную функцию системы по возмущающему воздействию (3).
Исходя из рис.4 передаточная функция по возмущающему воздействию
| (5.1) |
Подставив выражения (3.5) и (3.11) в выражение (5.1) получим искомую функцию в таком виде:
| (5.2) |
Из уравнения (5.2) имеем:
![]()
Следовательно
| (5.3) |
Тогда используя оператор смещения, можно перейти к разностному уравнению вида:
| (5.4) |
Рассмотрим качества управления при настройках ПИ-регулятора, выбранных из области устойчивости (рис.5):
K1 = 5, а K2 = 2.
Подставив K1 = 5, K2 = 2, а = 0,930 и b = 0,210 в уравнение (5.4), получим
| (5.5) |
Будем считать, что до подачи возмущающего воздействия в систему никаких отклонений выходной переменной y(t) не было, т.е.
| (5.6) |
Возмущающее воздействие f(t) согласно задания имеет вид (3). В дискретные моменты времени она соответственно принимает такие значения:
| (5.7) |
Изменения аргумента n = 0, 1, 2, 3, … и подставляя в правую часть уравнения (5.4) известные значения перменных, получим изменение выходной переменной во времени t.
Расчеты сведены в табл.1, а по ней на рис.6 приведен график изменения уровня жидкости в сборнике уровня жидкости при скачкообразном изменении возмущающего воздействия.
Таблица 1.
n | f(n) | f(n-1) | F(n-2) | y(n-1) | y(n-2) | y(n)= 0,88y(n–1)– – 0,51y(n–2)+f(n)– – 1,93f(n–1)+0,93f(n–2) |
0 | 0 | 0 | 0 | 0 | 0 | y(0) = 0 |
1 | 0,5 | 0 | 0 | 0 | 0 | y(1) = 0,88∙0 – 0,51∙0+ 0,5– – 1,93∙0+ 0,93∙0 = 0,5 |
2 | 0,5 | 0,5 | 0 | 0,5 | 0 | y(2) = – 0,025 |
3 | 0,5 | 0,5 | 0,5 | -0,035 | 0,5 | y(3) = – 0,277 |
4 | 0,5 | 0,5 | 0,5 | -0,383 | -0,035 | y(4) = – 0,231 |
5 | 0,5 | 0,5 | 0,5 | -0,319 | -0,383 | y(5) = – 0,062 |
6 | 0,5 | 0,5 | 0,5 | -0,085 | -0,319 | y(6) = 0,063 |
7 | 0,5 | 0,5 | 0,5 | 0,088 | -0,085 | y(7) = 0,087 |
5.2. Расчет переходного процесса в системе управления при изменении задающего воздействия.
Рассмотрим случай, когда задающее воздействие в системе управления уровнем жидкости есть единичное скачкообразное возмущение (ступенчатая функция) вида:
| (5.8) |
В z-форме (1) данное задающее воздействие имеет такой вид:
| (5.9) |
Передаточная функция системы по задающему воздействию определяется так
| (5.10) |
Подставив выражение (3.5) и (3.11) в выражение (5.10) получим передаточную функцию системы по задающему воздействию
| (5.11) |
Отсюда изображение выходной переменной, т.е. уровня жидкости, можно определить таким образом
![]()
| (5.12) |
Так как согласно Технического задания
| (5.13) |
Разделив числитель на знаменатель, получим ряд Лорана, коэффициенты которого есть значения уровня жидкости в САУ уровнем жидкости в дискретные моменты времени:
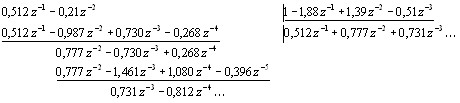
т.е. y(z) = 0 ∙ z + 0,525z-1 + 0,777z-2 + 0,731z-3 +…
Таким образом, изменения выходной переменной, вычисленное по этой схеме, сведены в табл.2.
Таблица 2n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y(n) | 0 | 0,525 | 0,777 | 0,731 | 0,562 | 0,437 | 0,414 | 0,458 | 0,508 |
По данным табл.2 на рис.7 приведены переходный процесс изменения уровня жидкости в САУ уровнем жидкости при скачкообразном изменении задающего воздействия.
Установившееся значение выходной переменной может быть найдено согласно уравнения (5.12) таким образом:
![]()
Или
| (5.15) |
Так как
![]()
Рассмотрим случай, когда задающее воздействие носит (имеет) синусоидальный характер, т.е. когда согласно ТЗ
| (5.16) |
Определим амплитуду выходной переменной (т.е. уровня жидкости) способом, описанным в (1). Для этого найдем мнимую и вещественную части передаточной функции системы по задающему воздействию. Подставим в выражение (5.11) ![]() . Тогда
. Тогда
![]()
или
| (5.17) |
где
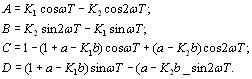
При ![]() передаточная функция замкнутой системы
передаточная функция замкнутой системы
| (5.12) |
а модуль![]()
Отсюда амплитуда выходной переменной
![]()
5.3. Выводы
1. При действии на систему автоматического управления единичного скачкообразного возмущающего воздействия были получены такие характеристики:
- длительность переходного процесса tp = 40;
- максимальное динамическое отклонение (ошибка) y1 = 0,5;
- затухание переходного процесса
2. При подаче в систему автоматического управления уровня жидкости единичного скачкообразного задающего воздействия были получены такие ее характеристики:
- длительность процесса управления ty = 2;
- перерегулирование
3. Амплитуда изменения уровня жидкости при синусоидальном изменении задающего воздействия на частоте составила 0,475.
ЛИТЕРАТУРА
- Кваско М.З. Проектирование и расчет цифровых систем управления. – К.: УМК АО, 1991. – 220 с.
- Справочник по автоматизации целлюлозно-бумажных предприятий (Э.В.Целиковский, Н.С. Пиргач, Г.Д. Ерашкин и др. – 3-е изд., перераб. и доп. – М.: Лесная промышленность, 1989. – 368 с.
- Пиргач Н.С., Пиргач В.С. Автоматическое регулирование и регуляторы в целлюлозно-бумажной и деревообрабатывающей промышленности. М.: Лесная промышленность, 1975, - 296 с.
 .
.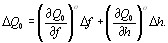
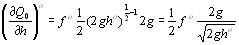
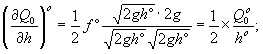

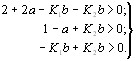 .
. .
.